前言
如果有数学基础,对高等数学中的微积分很熟悉,入门控制学会相对较快。可以看知乎的 小潘是个工程师 的专栏,过几遍他的文章,心中的框架自然而然的就建立起来了,说的很透彻,也正是以前和师弟所说,控制某种程度上就是求解微分方程,只不过自己很难解释的清楚,另一方面自己水平太低,也解释不清。作为自己的学习笔记,会将书中看到的一些重要的,记录在这里。
线性系统的基本特性
用线性微分方程描述的元件或系统,称为线性元件或线性系统。线性系统的重要性质是可以应用叠加原理。叠加原理有两重含义,即具有可叠加性和均匀性(或齐次性)。现举例说明∶设有线性微分方程
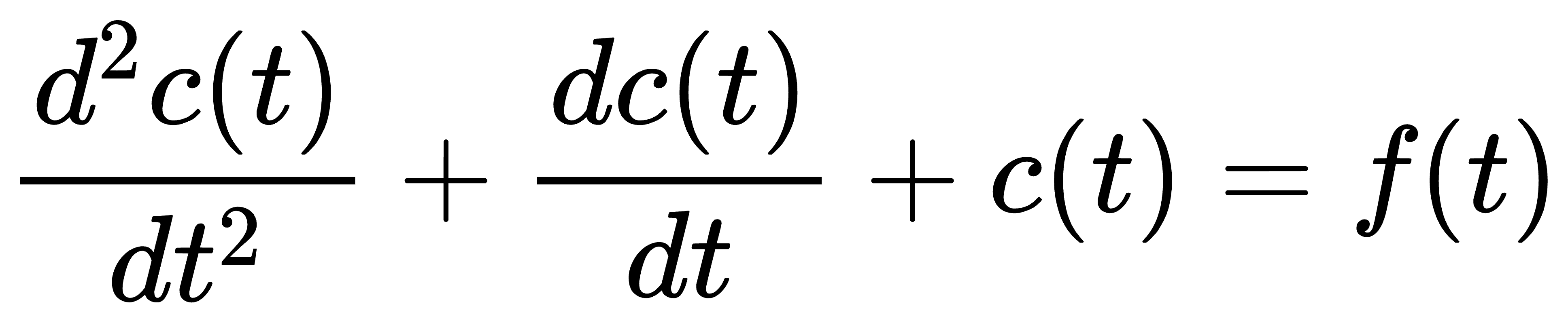
当f(t) = f1(t)时,上述方程的解为 c1(t); 当f(t) = f2(t),其解为c2(t). 如果 f(t) = f1(t) + f2(t), 容易验证,方程的解必为 c(t) = c1(t) +c2(t).这就是可叠加性。而当f(t) = Af1(t)时,式中A为常数,则方程的解必为 c(t) = Ac1(t), 这就是齐次性。
线性系统的叠加原理表明,两个外作用同时加于系统所产生的总输出,等于各个外作用单独作用时分别产生的输出之和,且外作用的数值增大若干倍时,其输出亦相应增大同样的倍数。因此,对线性系统进行分析和设计时,如果有几个外作用同时加于系统,则可以将它们分别处理,依次求出各个外作用单独加入时系统的输出,然后将它们叠加。此外,每个外作用在数值上可只取单位值,从而大大简化了线性系统的研究工作。
控制系统的复数域数学模型
控制系统的微分方程是在时间域描述系统动态性能的数学模型,在给定外作用及初始条件下,求解微分方程可以得到系统的输出响应。这种方法比较直观,特别是借助于计算机可以迅速而准确地求得结果。但是如果系统的结构改变或某个参数变化时,就要重新列写并求解微分方程,不便于对系统进行分析和设计。
用拉氏变换法求解线性系统的微分方程时,可以得到控制系统在复数域中的数学模型——传递函数。传递函数不仅可以表征系统的动态性能,而且可以用来研究系统的结构或参数变化对系统性能的影响。经典控制理论中广泛应用的频率法和根轨迹法,就是以传递函数为基础建立起来的,传递函数是经典控制理论中最基本和最重要的概念。
传递函数的性质
1)传递函数是复变量s的有理真分式函数,具有复变函数的所有性质;m≤n,且所有系数均为实数。
2)传递函数是一种用系统参数表示输出量与输入量之间关系的表达式,它只取决于系统或元件的结构和参数,而与输入量的形式无关,也不反映系统内部的任何信息。
3)传递函数与微分方程有相通性。传递函数分子多项式系数及分母多项式系数,分别与相应微分方程的右端及左端微分算符多项式系数相对应。故在零初始条件下,将微分方程的算符d/dt用复数s置换便得到传递函数;反之,将传递函数多项式中的变量s用算符d/dt置换便得到微分方程。
传递函数的极点和零点对输出的影响
由于传递函数的极点就是微分方程的特征根,因此它们决定了所描述系统自由运动的模态,而且在强迫运动中(即零初始条件响应)也会包含这些自由运动的模态。
线性系统的时域分析法
在经典控制理论中,常用时域分析法、根轨迹法或频域分析法来分析线性控制系统的性能。显然,不同的方法有不同的特点和适用范围,但是比较而言,时域分析法是一种直接在时间域中对系统进行分析的方法,具有直观、准确的优点,并且可以提供系统时间响应的全部信息。
动态过程与稳态过程
在典型输入信号作用下,任何一个控制系统的时间响应都由动态过程和稳态过程两部分组成。
(1) 动态过程
动态过程又称过渡过程或瞬态过程,指系统在典型输人信号作用下,系统输出量从初始状态到最终状态的响应过程。由于实际控制系统具有惯性、摩擦以及其他一些原因,系统输出量不可能完全复现输入量的变化。根据系统结构和参数选择情况,动态过程表现为衰减、发散或等幅振荡形式。显然,一个可以实际运行的控制系统,其动态过程必须是衰减的。
(2) 稳态过程
稳态过程指系统在典型输入信号作用下,当时间t趋于无穷时,系统输出量的表现方式。稳态过程又称稳态响应,表征系统输出量最终复现输人量的程度,提供系统有关稳态误差的信息,用稳态性能描述。
应当指出,由于所研究的系统实质上都是线性化的系统,称为线性逼近,在建立系统线性化模型的过程中略去了许多次要因素,同时系统的参数又处于不断地微小变化之中,所以临界稳定现象实际上是观察不到的。基于线性逼近的稳定性,李雅普诺夫证明了一个显著的结论;如果其线性逼近是严格稳定的,即所有的根在左半平面,那么非线性系统将在应用线性逼近的平衡点的某个邻域内稳定。此外,他还证明了另一个结论;如果线性逼近至少有一个根在右半平面,那么这个非线性系统不可能在平衡点的任何邻域内稳定。
减小或消除稳态误差的措施
为了减小或消除系统在输人信号和扰动作用下的稳态误差,可以采取以下措施。
(1) 增大系统开环增益或扰动作用点之前系统的前向通道增益。 |
注: 在反馈控制系统中,设置串联积分环节或增大开环增益以消除或减小稳态误差的措施,必然导致降低系统的稳定性,甚至造成系统不稳定,从而恶化系统的动态性能。因此,权衡考虑系统稳定性、稳态误差与动态性能之间的关系,便成为系统校正设计的主要内容。
(3)采用串级控制抑制内回路扰动
当控制系统中存在多个扰动信号,且控制精度要求较高时,宜采用串级控制方式,可以显著抑制内回路的扰动影响。
(4)采用复合控制方法
如果控制系统中存在强扰动,特别是低频强扰动,则一般的反馈控制方式难以满足高稳态精度的要求,此时可以采用复合控制方式。 复合控制系统是在系统的反馈控制回路中加入前馈通路,组成一个前馈控制与反馈控制相结合的系统,只要系统参数选择合适,不但可以保持系统稳定,极大地减小乃至消除稳态误差,而且可以抑制几乎所有的可量测扰动,其中包括低频强扰动。
线性系统的根轨迹法
根轨迹简称根迹,它是开环系统某一参数从零变到无穷时,闭环系统特征方程式的根在s平面上变化的轨迹。当闭环系统没有零点与极点相消时,闭环特征方程式的根就是闭环传递函数的极点,常简称之为闭环极点。因此,从已知的开环零、极点位置及某一变化的参数来求取闭环极点的分布,实际上就是解决闭环特征方程式的求根问题。当开环增益或其他参数改变时,其全部数值对应的闭环极点均可在根轨迹图上简便地确定。因为系统的稳定性由系统闭环极点唯一确定,而系统的稳态性能和动态性能又与闭环零、极点在s平面上的位置密切相关,所以根轨迹图不仅可以直接给出闭环系统时间响应的全部信息,而且可以指明开环零、极点应该怎样变化才能满足给定的闭环系统的性能指标要求。除此而外,用根轨迹法求解高阶代数方程的根,比用其他近似求根法简便。
离散状态方程求解
离散状态空间表达式中的状态方程实际上是一阶差分方程组,所以,关于差分方程求解的方法都可用于离散状态方程的求解,常用的方法有递推法和 z 变换法。
1, 递推法
设离散系统的状态空间表达式为
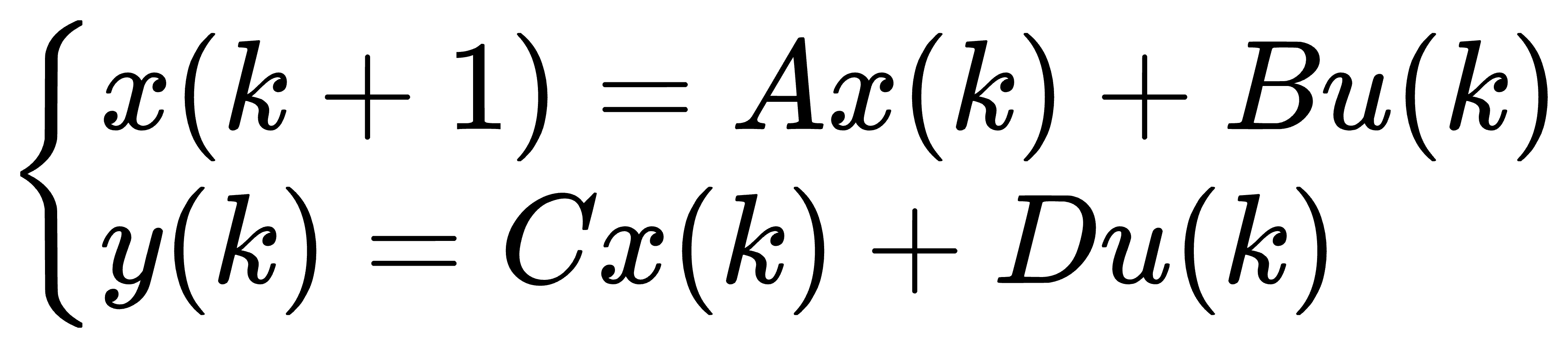
已知状态初始值 x(0) 和输入序列 u(k), 从 k=0 开始,按照状态方程逐步递推,就可得任意时刻的状态向量值。 对应的输出序列为
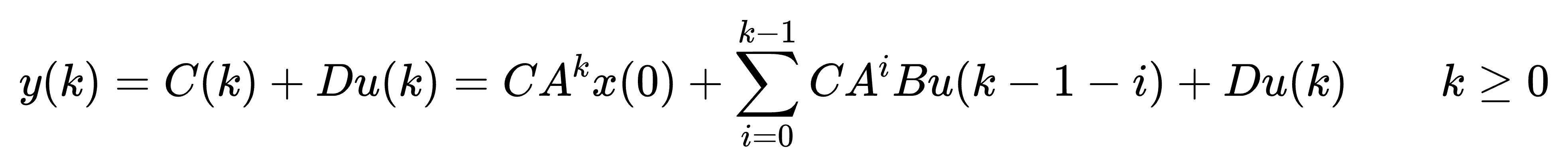
2, Z 变换法
对状态方程进行 z 变换,得
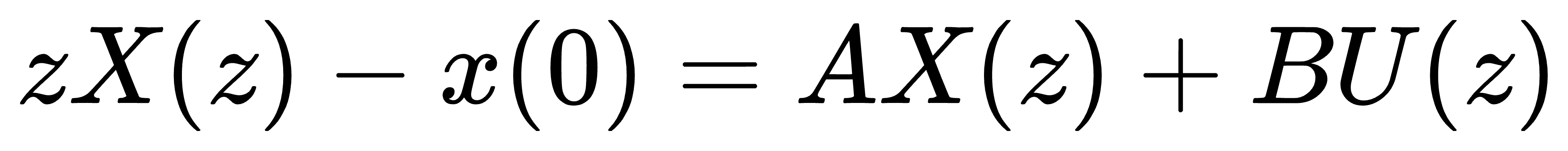
能控性和能观性
对于以离散状态空间表达的被控对象
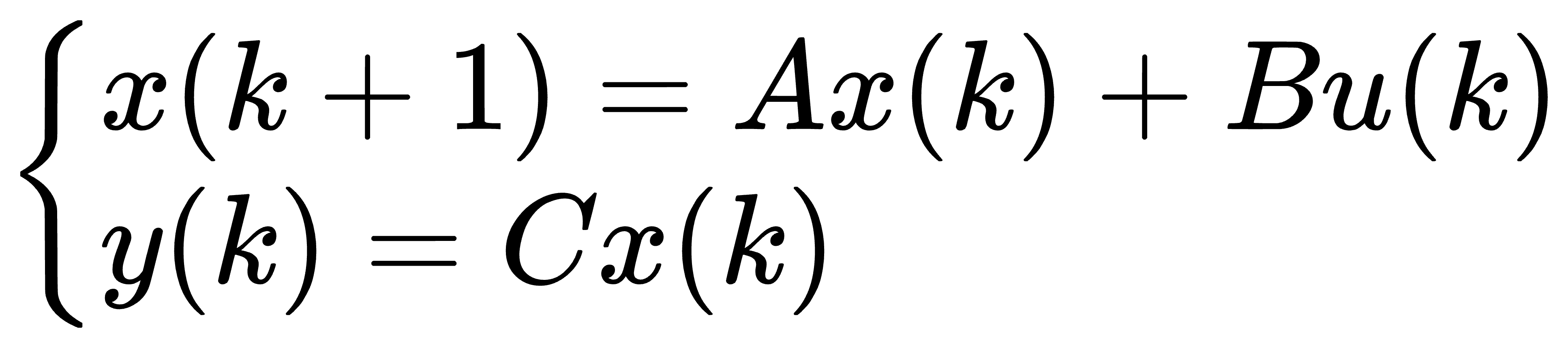
对上式进行z逆变换,即得状态向量序列

得到状态后,根据输出方程 y(k) = Cx(k) + Du(k)。求得输出序列。 用 z 变换法求解虽然复杂一些,但可以求得解析结果,可以获得所求序列的一般项的表达式。
对于以离散状态空间表达的被控对象
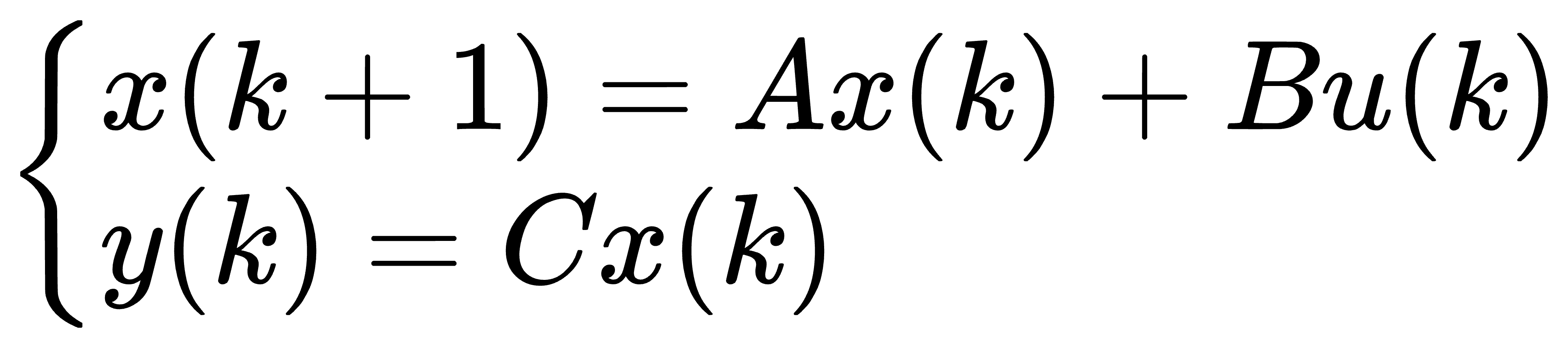
如果系统在一个有限的时间间隔内,可用一个无约束的控制向量,使得系统由初始状态 x(t0) 转移到终点状态或者回到原点 x(0),则称系统在时间 t0 是可控的。它说明了系统控制输人对系统内部状态的控制或影响的能力。
可控性是被控系统的内在属性,由系统的结构和参数所决定。如果一个被控系统没有可控性,则设计就失去了意义。可观测性是反映由系统的量确定系统状态的可能性,即是说通过分析测量,重构系统状态的可能性。如果一个系统在状态 x(t0),可通过在一个有限的时间间隔内,由输出量的观测值所确定,则称该系统在时间 t0 是可观测的,观测值取决于系统的特性 A 和 C. 实际上大多数系统是可控的和可观测的,但是也有部分物理系统不具有可控性和可观测性,因此要予以判断。
参考
[1] 《自动控制原理》 胡寿松
[2] 机电系统计算机控制
