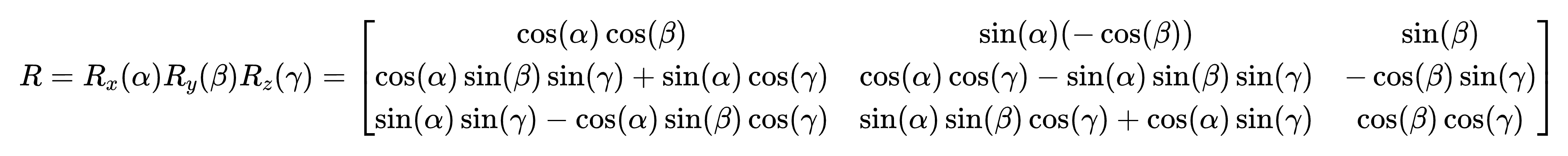• 欧拉角

欧拉角

欧拉角来描述刚体在三维欧几里德空间的姿态。对于任何参考系,一个刚体的姿态,在使用欧拉角的描述下可用三个基本旋转矩阵来决定。可用两个坐标系来解释,其中不动的坐标系作为参考,另外一个坐标系固定于刚体,随着刚体的旋转而旋转,就像下面所展示的那样

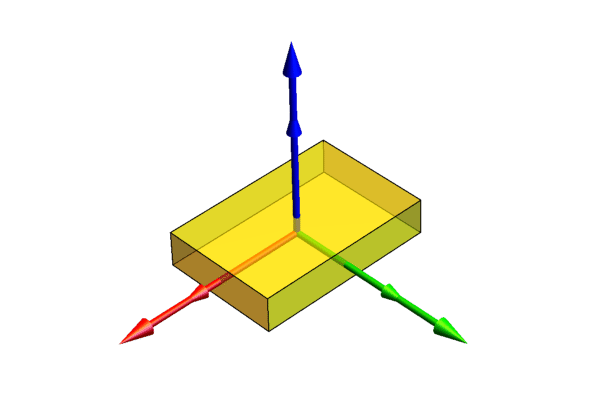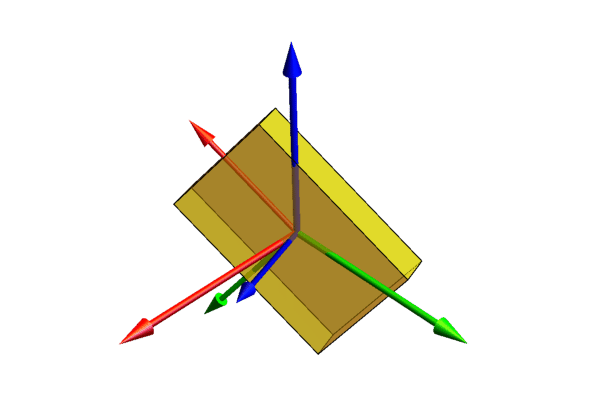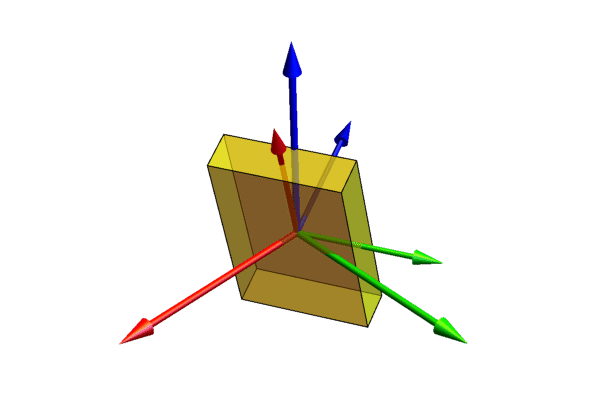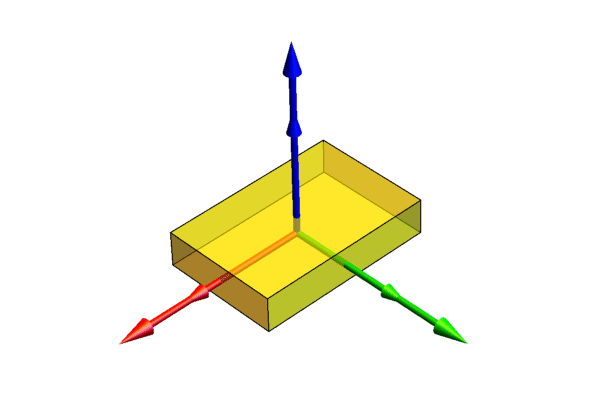
参考下图,设定xyz-轴为参考系的参考轴。称xy-平面与XY-平面的相交为交点线,用英文字母(N)代表。

zxz顺规的欧拉角可以静态地这样定义： 是x-轴与交点线的夹角, 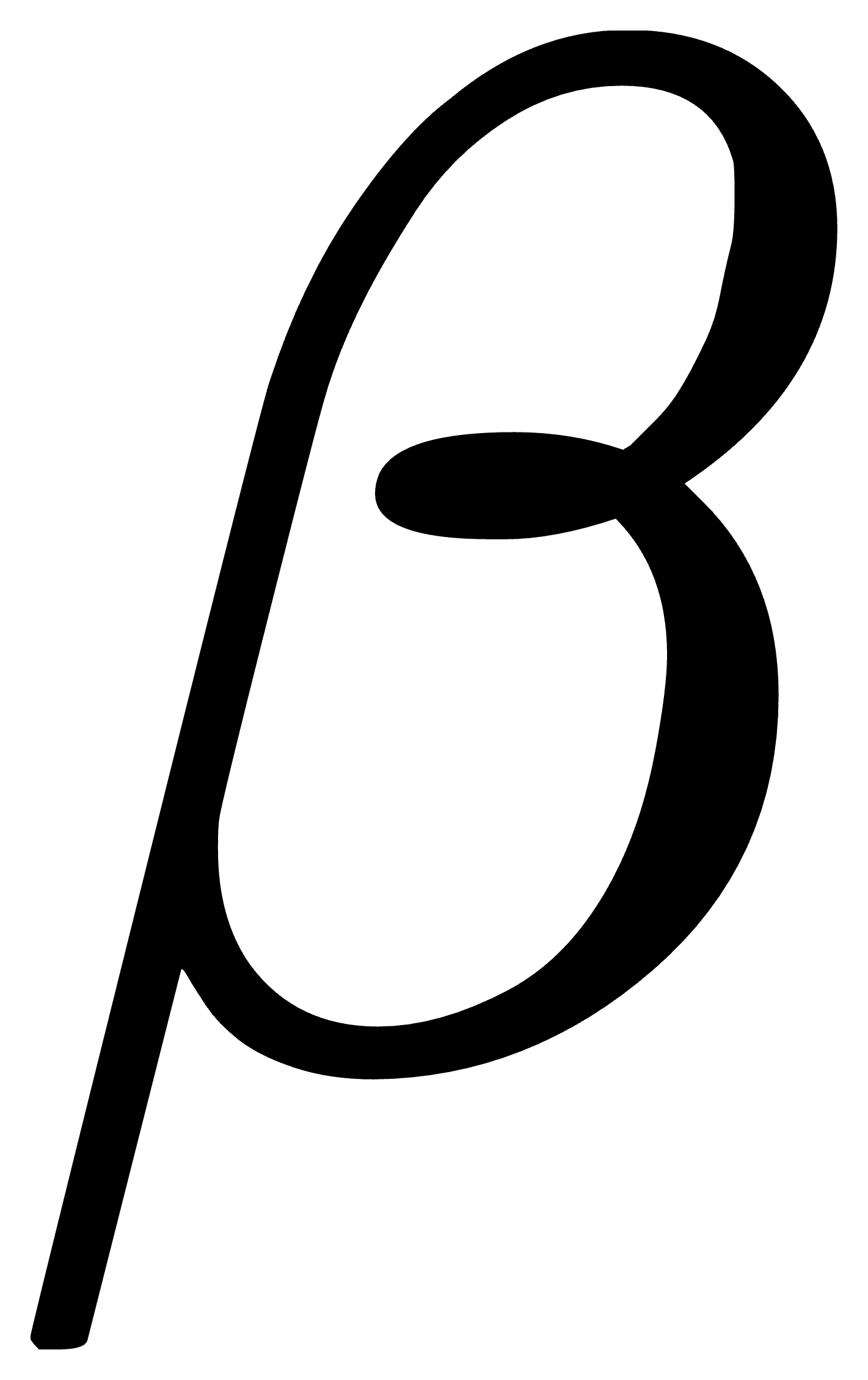是z-轴与Z-轴的夹角, 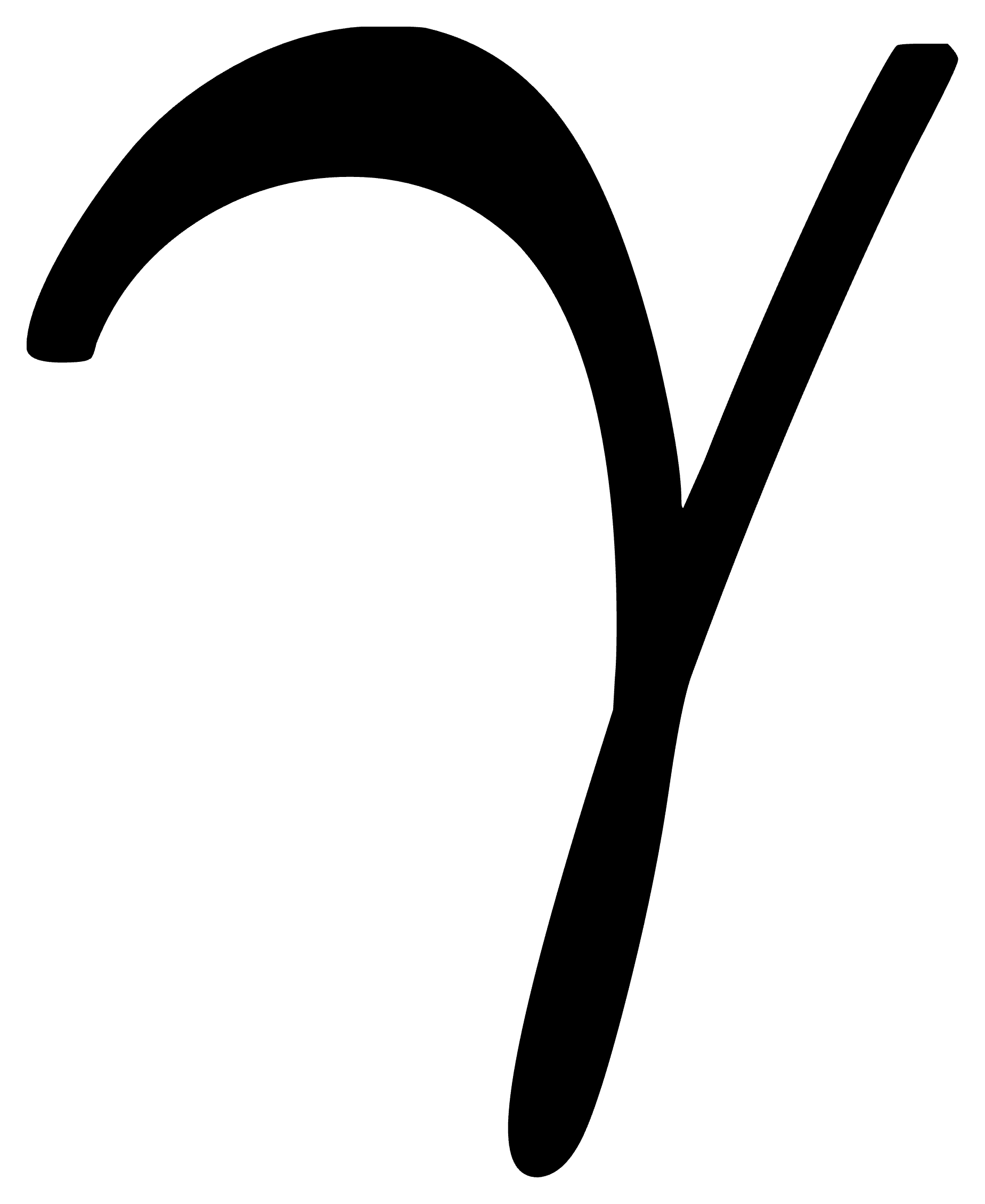是交点线与X-轴的夹角。

很可惜地,对于夹角的顺序和标记,夹角的两个轴的指定,并没有任何常规。科学家对此从未达成共识。每当用到欧拉角时,我们必须明确的表示出夹角的顺序,指定其参考轴。 实际上,有许多方法可以设定两个坐标系的相对取向。欧拉角(共有12组组合)方法只是其中的一种。此外,不同的作者会用不同组合的欧拉角来描述,或用不同的名字表示同样的欧拉角。因此,使用欧拉角前,必须先做好明确的定义。

在RTB上默认采用的是横滚一俯仰一偏航角这种情况,其旋转矩阵为(需要注意的是rpy定义有多种,比如zyx,xyz等等, 常用的为ZYX欧拉角)