三环控制系统

前言
三闭环系统构成
系统的基本研究内容
- 典型系统
  - 典型Ⅰ型系统
  - 典型Ⅱ型系统
手动调整速度环增益和位置环增益
增益调整与机械刚性的关系
- 提高机械刚性
机器人关节带宽和测量
- 如何影响带宽
- 带宽的测量
参考

前言

之前记录的一部分笔记里,有关于运动控制的简单说明,这部分的内容还是非常吸引自己的,于是就查阅了相关的书本资料,做进一步的学习,下面很多内容/笔记是出自于孙宇等人编著的《交流伺服系统设计指南》,里面的内容让人眼前一亮,会让人对经典控制理论产生极大的兴趣,非常值得去好好的学习下。内容仅作为学习使用,会穿插一些自己对内容的理解以及相关的代码演示等。

三闭环系统构成

高性能交流伺服控制系统通常具有位置反馈、转速反馈和电流反馈的三闭环结构形式, 如图所示。图中, 虚线框内表示电源、电动机及编码器模型, 其中 APR 表示位置调节器, ASR 表示转速调节器, ACR 表示电流调节器。

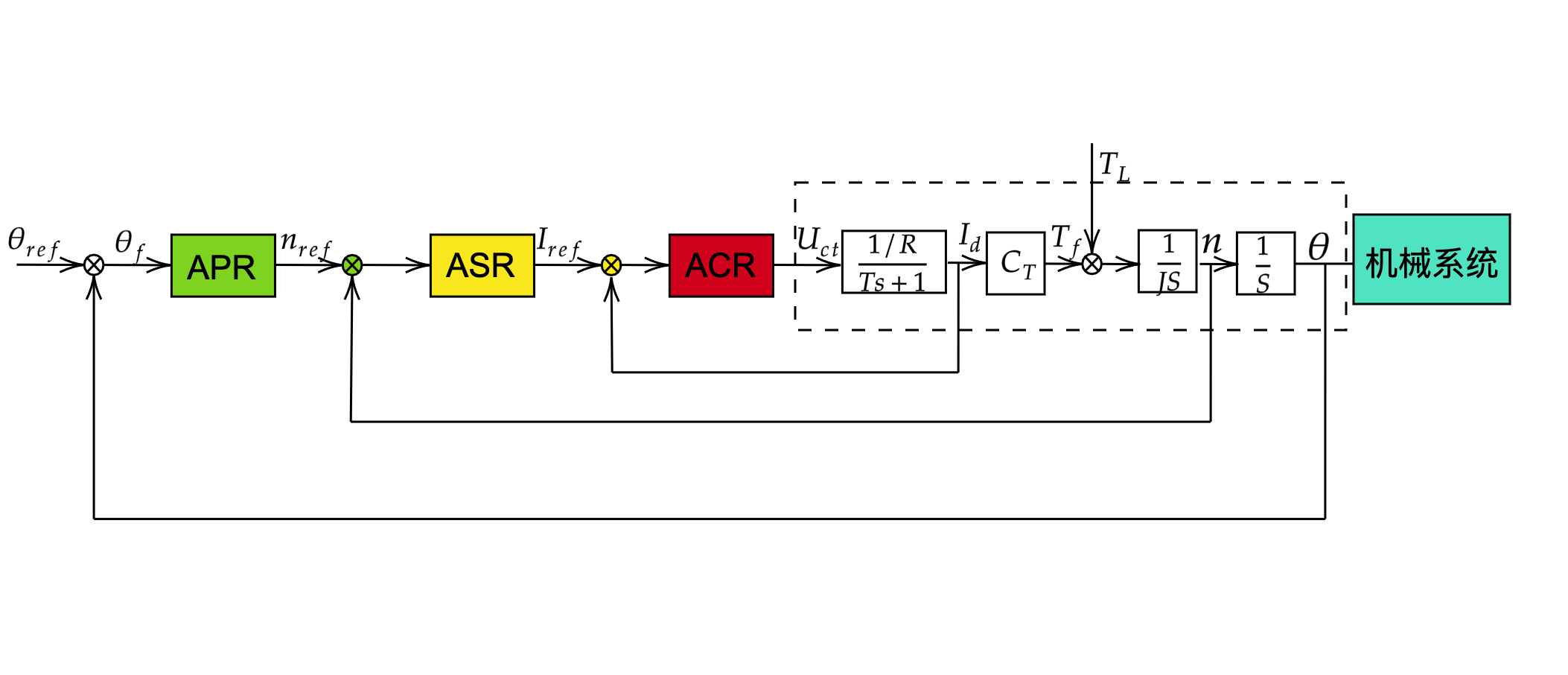
三个环路调节器都由 P 和 I 组成, 虽然结构相似, 但是完成的功能却各自不同：

① 电流环 ACR 的作用是改造内核控制对象的传递函数, 提高系统的快速性；及时抑制电流环内部的干扰；限制最大电流, 使系统有足够大的加速度转矩, 并且保障系统安全运行。

② 速度环 ASR 的作用是增强系统抗负载扰动的能力；抑制转速波动。

③ 位置环 APR 的作用是保证系统静态准确度、刚度和动态跟踪的性能；它是反馈的主要通道。

通常把电流环称为内环, 三个环的设计步骤由内到外, 即依次是电流环, 速度环和位置环。针对各个闭环的具体作用和要求, 采取相应的控制策略。首要考虑系统的稳定性, 此外, 系统的跟随性、扰动性、误差以及稳态裕度等性能也是考虑的基本内容。

机械系统是指系统负载和负载与电动机连接的机械传动机构的总称。通常假设电动机与机械系统的连接特性为理想化的刚性,如下图所示

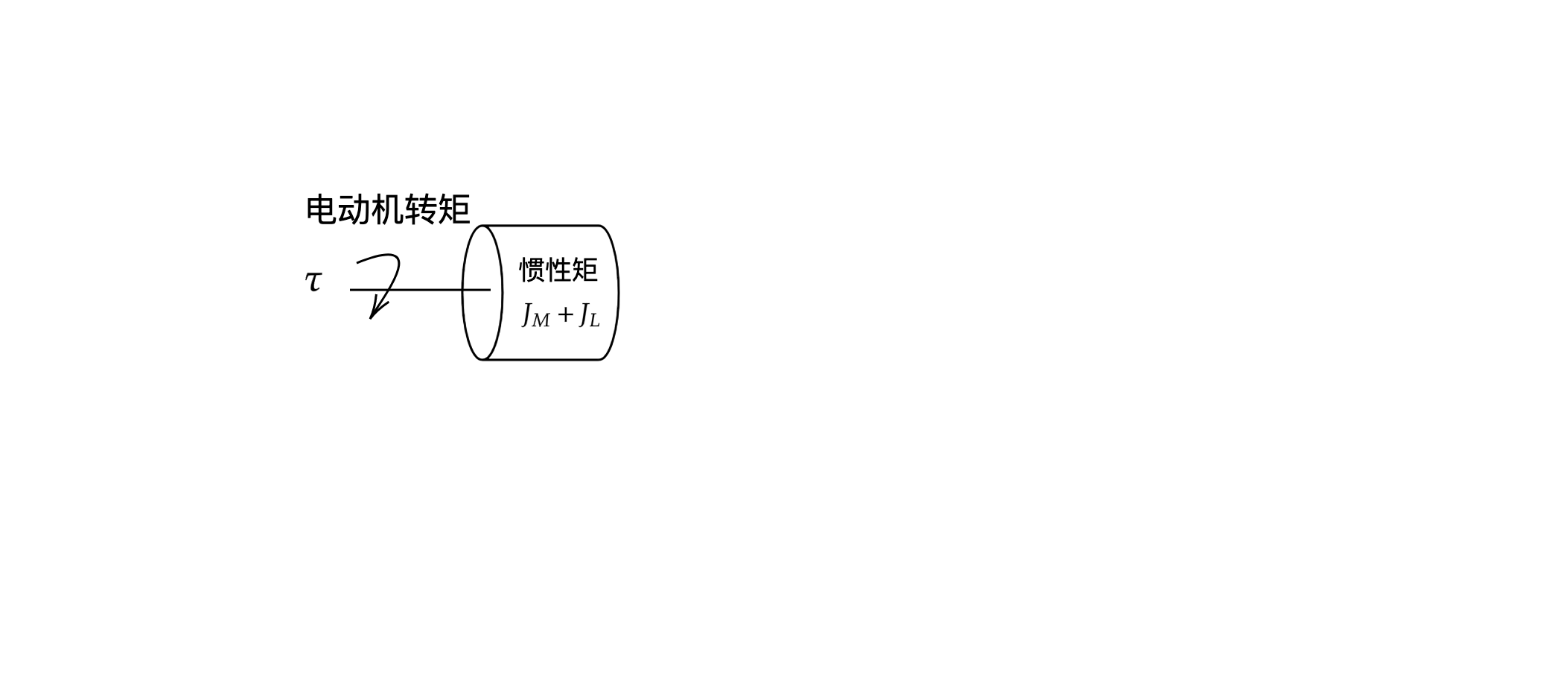
系统转动惯量 J 即是电动机转动惯量 JM 与负载转动惯量 JL 之和由它建立的系统一般称为单惯性系统。实际上,机械传动连接特性并非理想化的刚性,它存在一定的柔性,如下图所示,由它建立的系统称为两惯性系统。在该物理模型中,连接特性具有柔性耦合特性,存在弹性常数 Ks ,它使得系统转动惯量 J 不再是电动机转动惯量 JM 与负载转动惯量 JL 之和。更复杂的是,这种柔性耦合通常会在系统中引发机械振动,机械振动除了发出声学噪声形成噪声污染外,还会对机械传动装置造成严重的损害,影响其使用寿命。另外,甚至还会引发控制系统中的控制量振荡,使得闭环控制的稳定性以及可调整性受到制约。

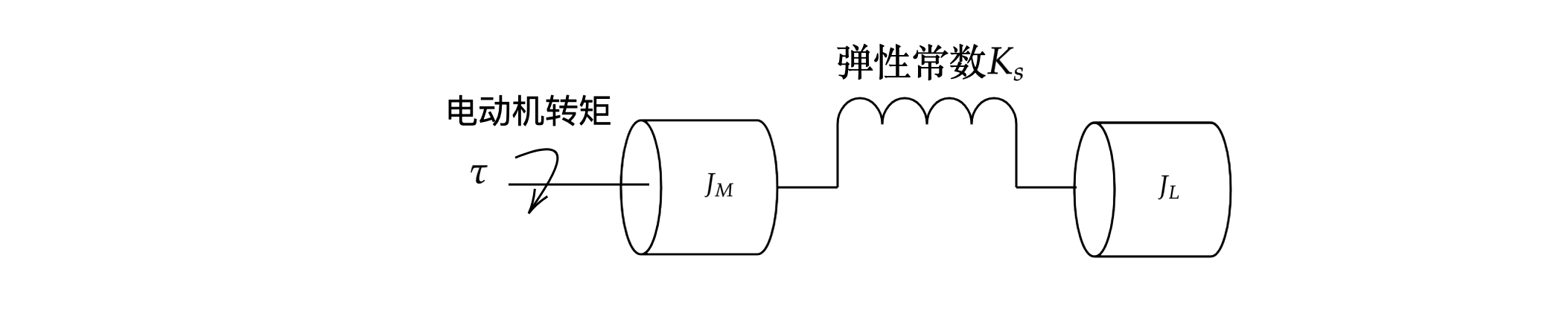
由经验可以得出, 虽然三闭环控制策略是在单惯性系统物理模型下分析得出的, 但它同样适用于振动负载模型, 其结论对实际应用中的伺服控制系统同样是有效的。因此主动式解决振动的方法多数也是在三闭环控制系统的基础上展开研究的。调整伺服系统就是通过调整各个环路的增益与滤波以使伺服控制器匹配机械特性,从而达到减小振动、快速跟踪指令并且消除异常噪音的目的。

系统的基本研究内容

稳定是控制系统的重要性能, 也是系统能够正常运行的首要条件。在交流伺服控制系统设计中, 分析三闭环结构是否稳定并不重要, 因为工业中即使是临界稳定的系统也是没有用的。对于设计人员来说, 花费大量精力的重点在于测量系统有多稳定, 或者准确地说在于测量系统所拥有的稳定性裕度有多大。无论是在工程应用中, 还是在理论研究上, 这里推荐大家使用相位裕度 (Phase Margin,PM) 和增益裕度 (Gain Margin, GM) 来作为系统稳定程度的度量。这是因为：

① PM 和 GM 是系统稳定性最直观的量度；

② 开环设计法是数字的, 适合于计算机；

③ 这种方法不需要对控制系统进行任何的简化性假设。

若统开环传递函数的对数频率特性曲线如下所示。图中,相位裕度(PM)(通常也称为相角裕度)定义为 180°加开环幅相曲线幅值为 1时的相位∶

$\gamma = 180^\circ + G(j\omega_c)H(j\omega_c)$

式中 $\omega_c$ 为系统的截止角频率。增益裕度 (GM, 通常也称为幅值裕度) 定义为幅相曲线上, 相位为 -180°时对应幅值的倒数：

$h=\frac{1}{|G(j\omega_g)H(j\omega_g)|}$

通常幅值裕度用分贝值 dB 表示, 将上面的式修改为

$h=20lg\frac{1}{|G(j\omega_g)H(j\omega_g)|} = -20lg|G(j\omega_g)H(j\omega_g)|$

虽然目标是测量 PM和 GM的值,但是确定这两个量度的期望值需要判断。其原因之一是裕度大小随应用要求的变化而变化。例如,有些必须跟随指令信号,如阶跃指令信号的场合,除了极稳定的系统外都会产生超调。相对于响应变化柔和的指令信号来说,这样的应用需要更高的稳定裕度。此外,与其他应用相比,有些应用可以承受更大的超调量。最后,对于同样的响应,有些控制方法需要比其他方法更大的相位裕度或者增益裕度。例如,对于一个阶跃响应来说,要获得相同的超调量,PI 调节器需要一定的相位裕度,而对于PID 调节器来说,较小的相位裕度就可能消除所有超调。经验表明,增益裕度(GM)应为10～ 25dB,而相位裕度(PM)应为35°~80°,这取决于具体应用及控制器类型。一般情况下,幅值裕度越大越好,同样,相角裕度也是越大越好。由于增益穿越处及其附近的相位滞后降低了相位裕度, 于是在整个控制回路中的每个噪声滤波器、反馈装置以及功率变换器均带来了相位滞后, 每个相位滞后都侵蚀相位裕度, 没必要的相位滞后限制了调节器的最终性能。因此, 一条最基本的控制法则是：消除没必要的相位滞后。

典型系统

一般来说, 系统的开环传递函数都可表示为

$W(s) = \frac{K(\tau_1s+1)(\tau_2s+1)}{s^r(T_1s+1)(T_2s+1)}$

式中,分子和分母上都可能含有复数零点和复数极点诸项。分母中的s’项表示系统在原点处有r重极点,或者说,系统含有r个积分环节。根据r=0,1,2,…不同值,分别称为0型、Ⅰ型、Ⅱ型、…系统。自动控制理论证明,0型系统在稳态时是有差的,而Ⅲ型和Ⅲ型以上的系统很难稳定。因此,通常为保证稳定性和一定的稳态准确度,多用I型和Ⅱ型系统。

典型Ⅰ型系统

作为典型Ⅰ型系统, 其开环传递函数选择为

$W(s) = \frac{K}{s(Ts+1)}$

它的闭环系统结构如下所示,

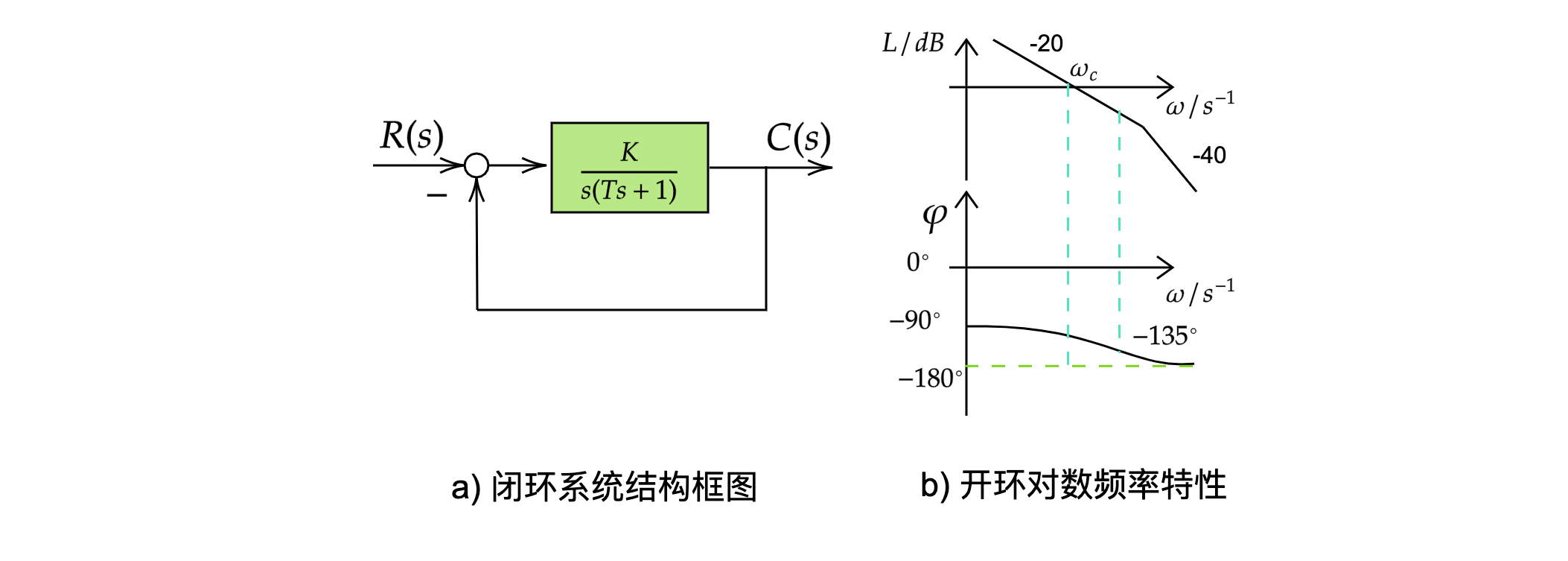
图 b 表示它的开环对数频率特性。选择它作为典型系统不仅因为其机构简单, 而且对数幅频特性的中频段以 - 20dB / dec 的斜率穿越零分贝线。只要参数的选择能保证有足够的中频带宽度,系统就一定是稳定的, 且有足够的稳定裕量。显然要做到这一点, 应有

$\begin{cases}\omega_c<\frac{1}{T}\\ arctan \omega_cT<45^\circ\end{cases}$

则相位稳定裕度有

$\gamma = 180^\circ - 90^\circ - arctan \omega_cT>45^\circ$

典型Ⅱ型系统

在Ⅱ型系统中,选择一种最简单而稳定的机构作为典型的Ⅱ型系统,其开环传递函数为

$W(s) = \frac{K(\tau s + 1)}{s^2(Ts+1)}$

它的闭环系统结构和开环对数频率特性如图所示,

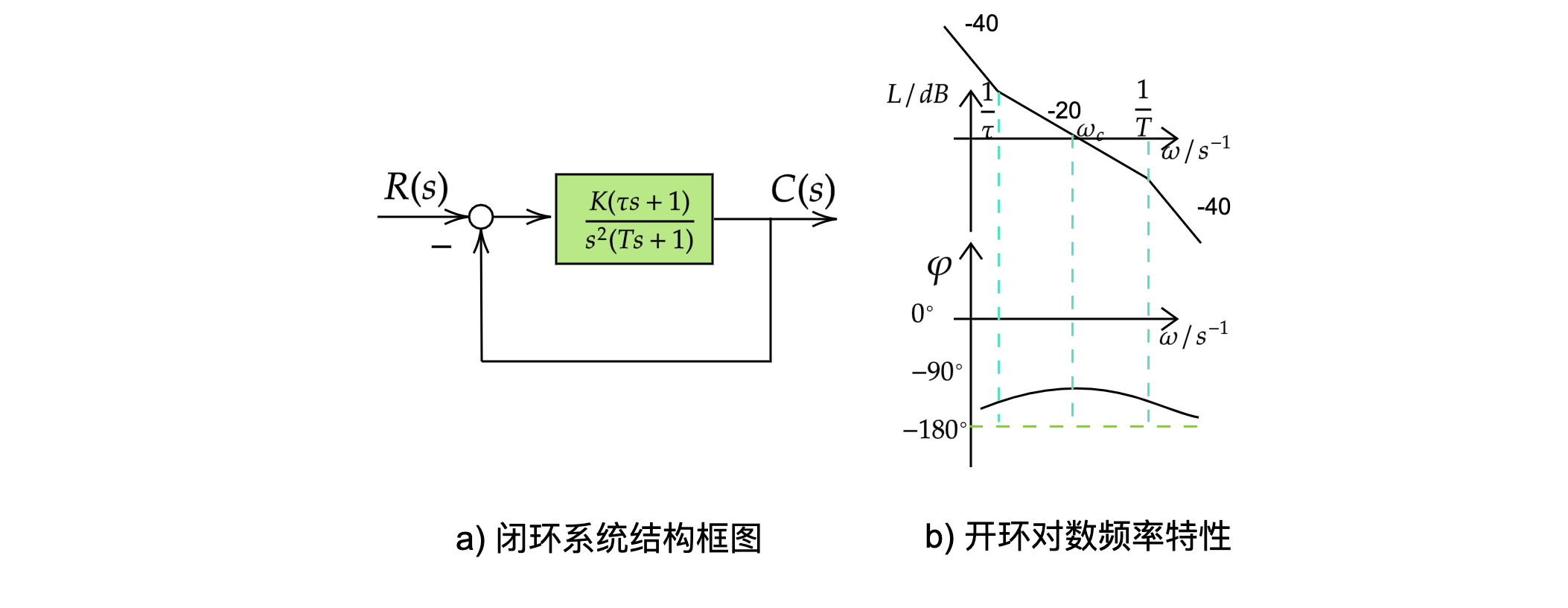
其中频段也是以 - 20dB / dec 的斜率穿越零分贝线。由于分母中已经有s²,对应的相频特性是-180°,后面还有一个惯性环节(这是实际系统必定有的),如果在分子上不添加一个比例微分环节 $(\tau s+1)$ ,就无法把相频特性抬到-180°线以上去,也就无法保证系统稳定。要实现图b这样的特性,显然应有

$\begin{cases}\frac{1}{\tau}<\omega_c<\frac{1}{T}\\ \tau>T\end{cases}$

则相位稳定裕度为

$\gamma = arctan \omega_c \tau - arctan \omega_cT$

由上式可得到, $\tau$ 比T大得越多,则稳定裕度越大。

手动调整速度环增益和位置环增益

这部分的内容,松下的伺服驱动器手册说的是非常的详细的,结合着自己查阅相关驱动器手册,对其进行一点归纳。

伺服驱动器首要的性能参数调整有三个：1.速度环增益；2.速度环积分时间常数;3.位置环增益。

增益调整与机械刚性的关系

提高机械刚性

1,应将机械牢固的置于地基上,使之不产生晃动。

2,应使用刚性高的伺服联轴器。

3, 使用宽幅的同步带。此外,张力应在电机容许轴向的过负载范围内。

4, 使用齿隙小的齿轮。机械部相关的固有振动 (共振频率) 会极大影响伺服机械的增益调整。共振频率低的机械 (=机械刚性低) ,伺服相关的响应性不可以设定过高。

机器人关节带宽和测量

文章写的很好，就直接搬运，下面为搬运的内容；

电机的伺服驱动器通常包括三种控制环——位置环、速度环和电流环。虽然每种控制环的目的是控制电机性能的不同方面，但它们都有一个共同的参数：带宽。在伺服驱动器中，带宽定义为闭环频率响应幅度大于 -3dB 的频率范围。此时，输出增益约为幅值的70.7%，输出功率等于输入功率的50%。定性地讲，系统的带宽可以衡量它对不断变化的输入命令的响应速度，因此对机器人的控制性能至关重要。

在协作机械臂和腿足式机器人中，位置带宽和力矩带宽已经成为衡量其伺服关节性能的重要指标：

位置带宽：描述执行器可以有效跟踪期望轨迹的最大频率，单位Hz，通常以峰值最大速度为指标来评价。
力矩带宽：描述执行器可以有效跟踪期望力矩的最大频率，单位Hz，通常以峰值最大扭矩为指标来评价。

一些典型的力控关节带宽指标如下表所示。

关节	力矩带宽（Hz）	测试负载 (Nm)	力检测方式
ETH ANYdrive [1]	＞60	1 Nm	SEA
iit WALK-MAN actuator [2]	14.24	35 Nm	SEA
iit WALK-MAN actuator [2]	28.05	35 Nm	Torque sensor
Blue Module [3]	13.8	10 Nm	QDD+电流检测

如何影响带宽

关节都可以近似看成一个二阶质量-弹簧-阻尼系统，因此这三者会对系统力矩带宽产生影响。下面是我以JTS-based关节的闭环传递函数为例，分析这三个参数对力矩带宽影响的仿真结果。

关节整体刚度：刚度越高，带宽越高
传动系统惯量：惯量越小，带宽越高
负载端阻尼：阻尼越大，带宽越高

由于传动系统惯量和负载端阻尼很难在设计关节时人为设定，因此大多数工作都是从关节刚度入手来改变力矩带宽。

带宽的测量

确定幅值

由于力矩带宽的具体大小由关节输出端负载决定，因此在测量时需要根据你的期望力矩幅值来测量相应带宽。

3.2 生成扫频信号

实验时需要根据实际经验大致定义关节力矩带宽的范围，比如0-60Hz，然后在规定时间内给控制器输入频率随时间变化的力矩信号。下面代码是以Matlab语言为例，在0-10s内生成0-60Hz，幅值为A的信号，具体使用时转换为相应的控制器程序语言写入控制器即可

% 使用数学函数式生成啁啾信号
fs = 1000;              % 控制器采样频率，1KHz
f_ini = 0;              % 初始频率,单位Hz
f_fin = 60;             % 终止频率,单位Hz
dT = 10;                % 采样周期,单位s
t1= 0:1/fs:dT;          % 采样间隔
K= A*(f_fin-f_ini)/dT;  % 频率线性增长率, A为信号幅值
track = cos(2*pi*(f_ini.*t1+0.5.*K.*t1.*t1));

Matlab有自带的chirp函数可以生成余弦扫频信号，但是无法写入控制器，所以可以把chirp函数当作验证工具来来验证你的扫频信号。

实验装置及数据整理

1）实验开始前，需要通过机械装置锁住关节输出端；

2）实验时，关节工作在力矩模式（closed-loop），力矩环输入命令为扫频信号；

3）实验过程中实时记录当前信号频率和对应力矩幅值；

4）最后根据数据画bode图，找出-3dB对应的频率点，即为关节力矩带宽的截止频率。

参考

[1] 松下驱动器手册

[2] 机器人关节带宽的理解和测量