前言
对身为控制小白的我,由于工作的需要,不得不学经典控制理论里面的东西,进而对控制系统进行相关的设计,心里一直有个苦恼的地方就是怎么看懂Bode图,以及如何根据经典控制理论来设计控制器。同时也很想了解Bode图的绘制过程,以及如何从图中获取有用的信息,将从网络以及书本里获取到的有助于自己理解的内容,记录如下。
简介
伯德图是线性非时变系统的传递函数对频率的半对数座标图,其横轴频率以对数尺度表示,利用波德图可以看出系统的频率响应。
波德图幅频图的频率用对数尺度表示,增益部分一般都用功率的分贝值来表示,也就是将增益取对数后再乘以20。由于增益用对数来表示,因此一传递函数乘以一常数,在波德增益图只需将图形的纵向移动即可,二传递函数的相乘,在波德幅频图就变成图形的相加。幅频图纵轴0分贝以下具有正增益裕度、属稳定区,反之属不稳定区：
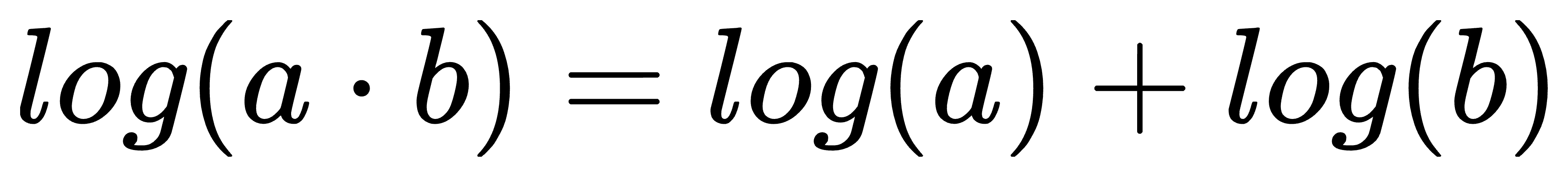
伯德图相频图的频率也用对数尺度表示,而相位部分的单位一般会使用度。配合波德相频图可以估算一信号进入系统后,输出信号及原始信号的比例关系及相位。例如一个A*sin(ω*t) 的信号进入系统后振幅变原来的k倍,相位落后原信号Φ,则其输出信号则为(A*k) sin(ω*t − Φ),其中的k和Φ都是频率的函数。相频图纵轴-180度以上具有正相位裕度、属稳定区,反之属不稳定区
开环传递函数的典型环节分解可将开环系统表示为若干个典型环节的串联形式
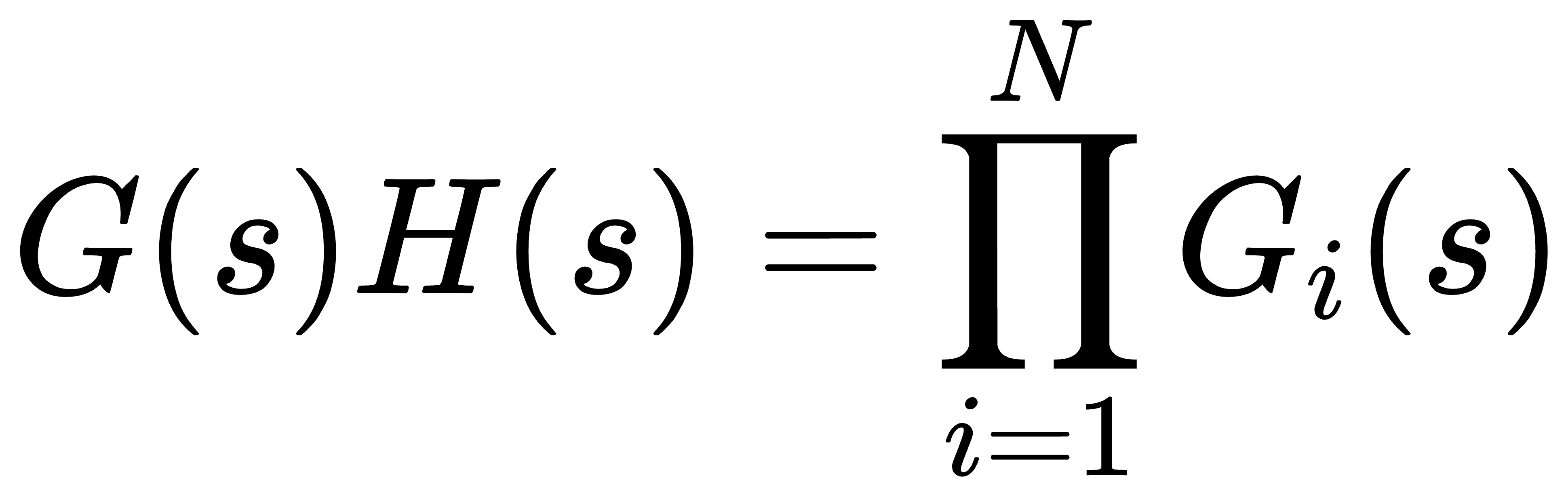
设典型环节的频率特性为
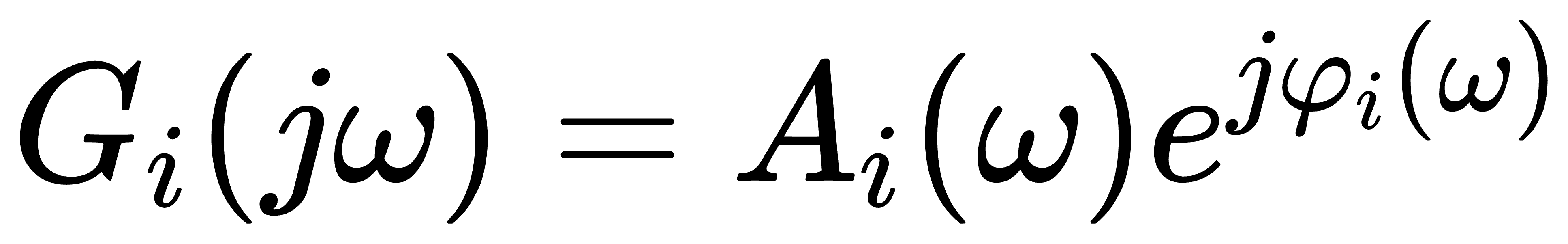
则系统开环频率特性
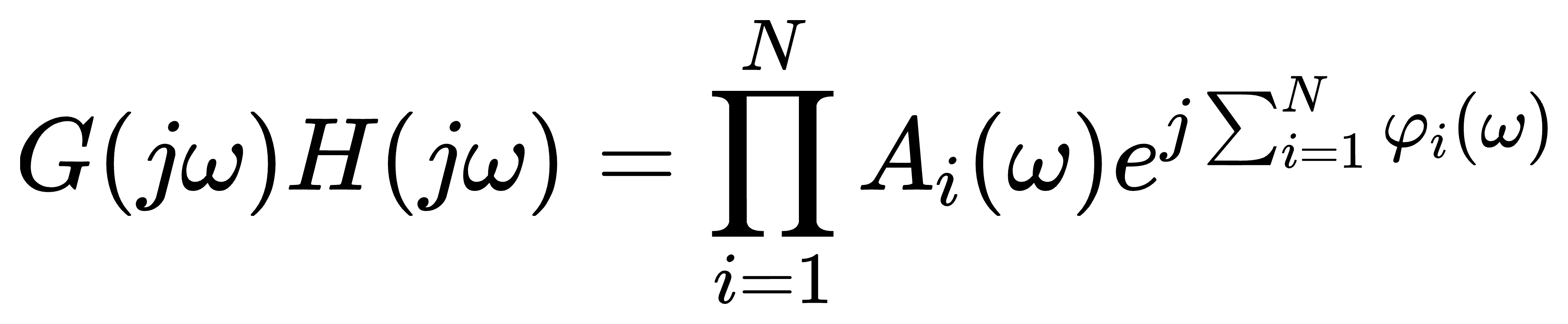
系统开环幅频特性和开环相频特性
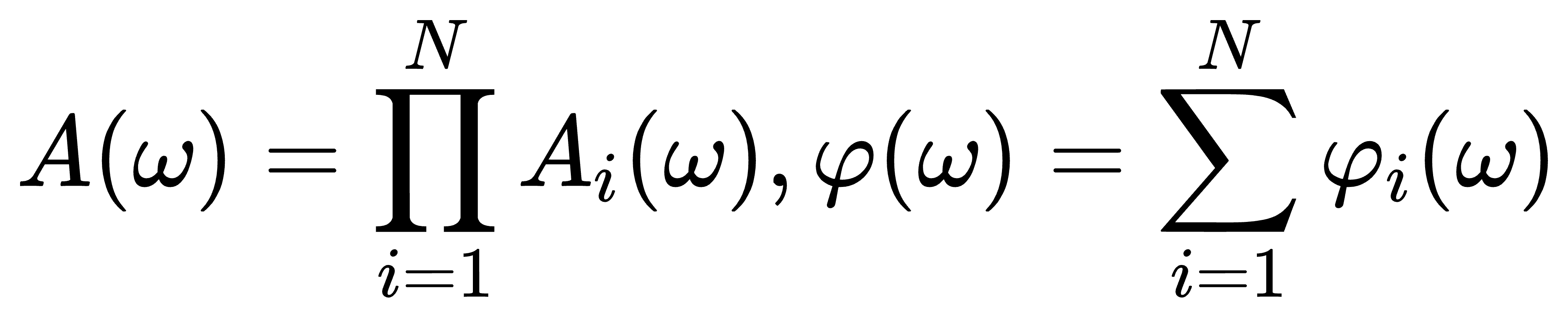
系统开环对数幅频特性
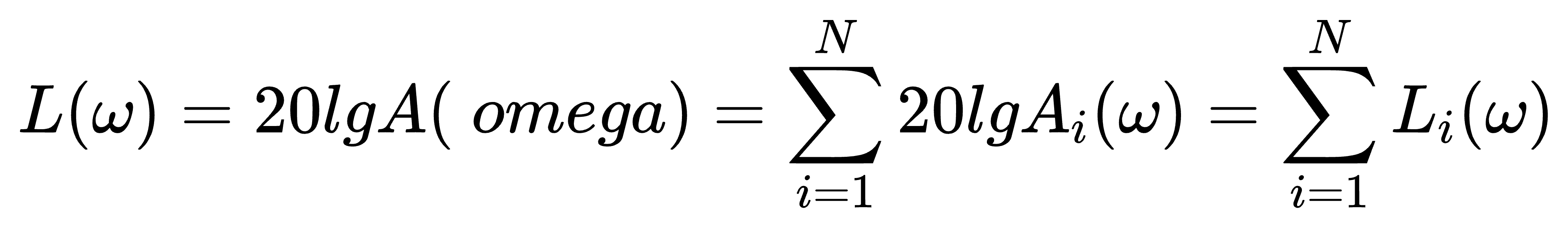
上面两个式子表明,系统开环频率特性表现为组成开环系统的典型环节频率特性的合成;而系统开环对数频率特性,则表现为典型环节对数频率特性叠加这一更为简单的形式。
若将系统的增益以复数表示,则复数增益取对数后的虚部即为相位,因此二传递函数的相乘,在波德相位图上也是图形的相加。若转换函数是有理函数,其零点及极点均为实数,则其波德图可以用几条渐近线的直线来近似,利用简单的规则即可以徒手绘制。若近似的波德图再修正每个截止频率时的增益值,则其近似值会更接近实际值。
波德图手绘的规则
波德图的前提就是可以处理以下型式函数的对数值：
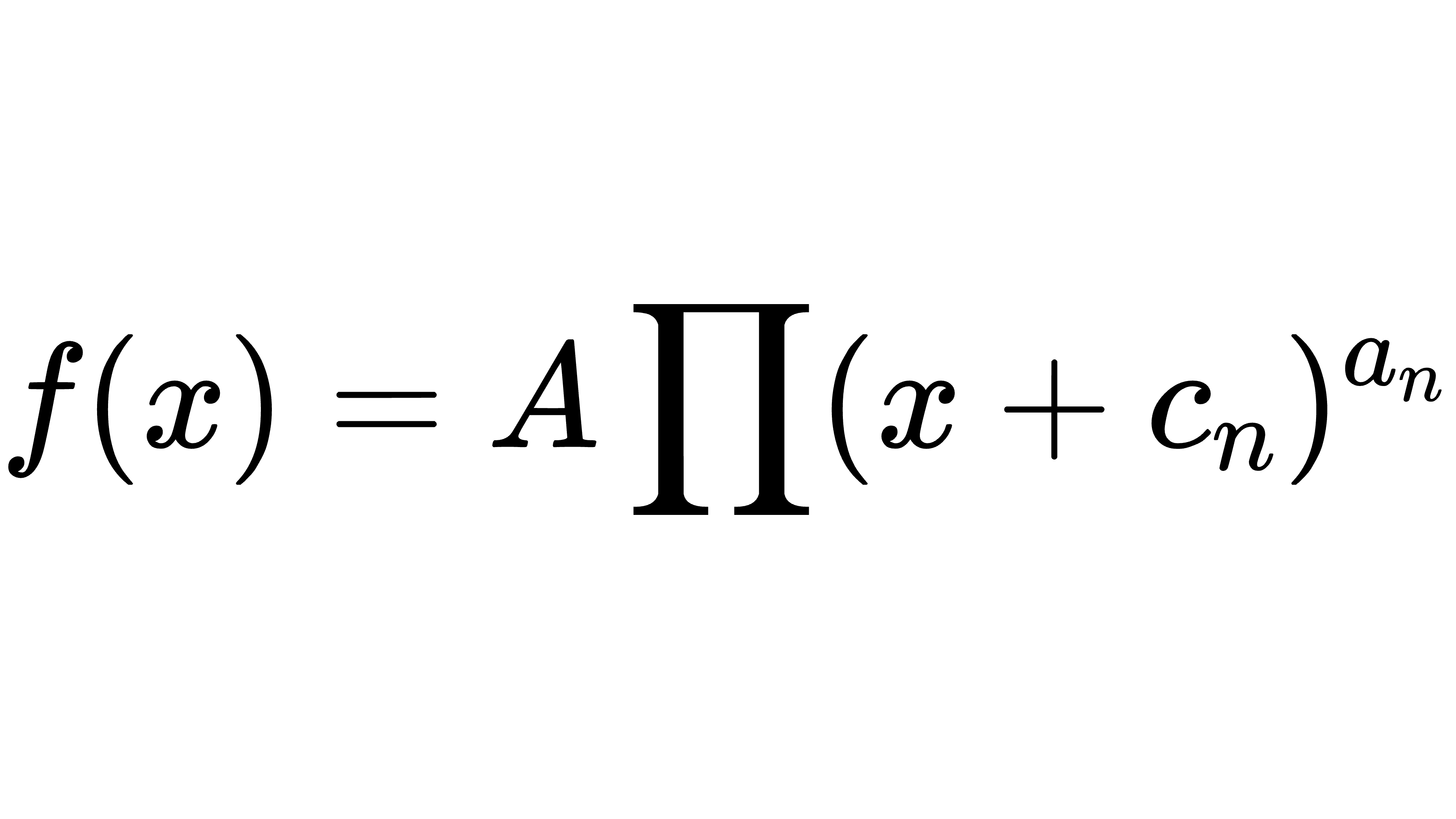
上述函数的对数值可以转换为极点及零点对数的和：
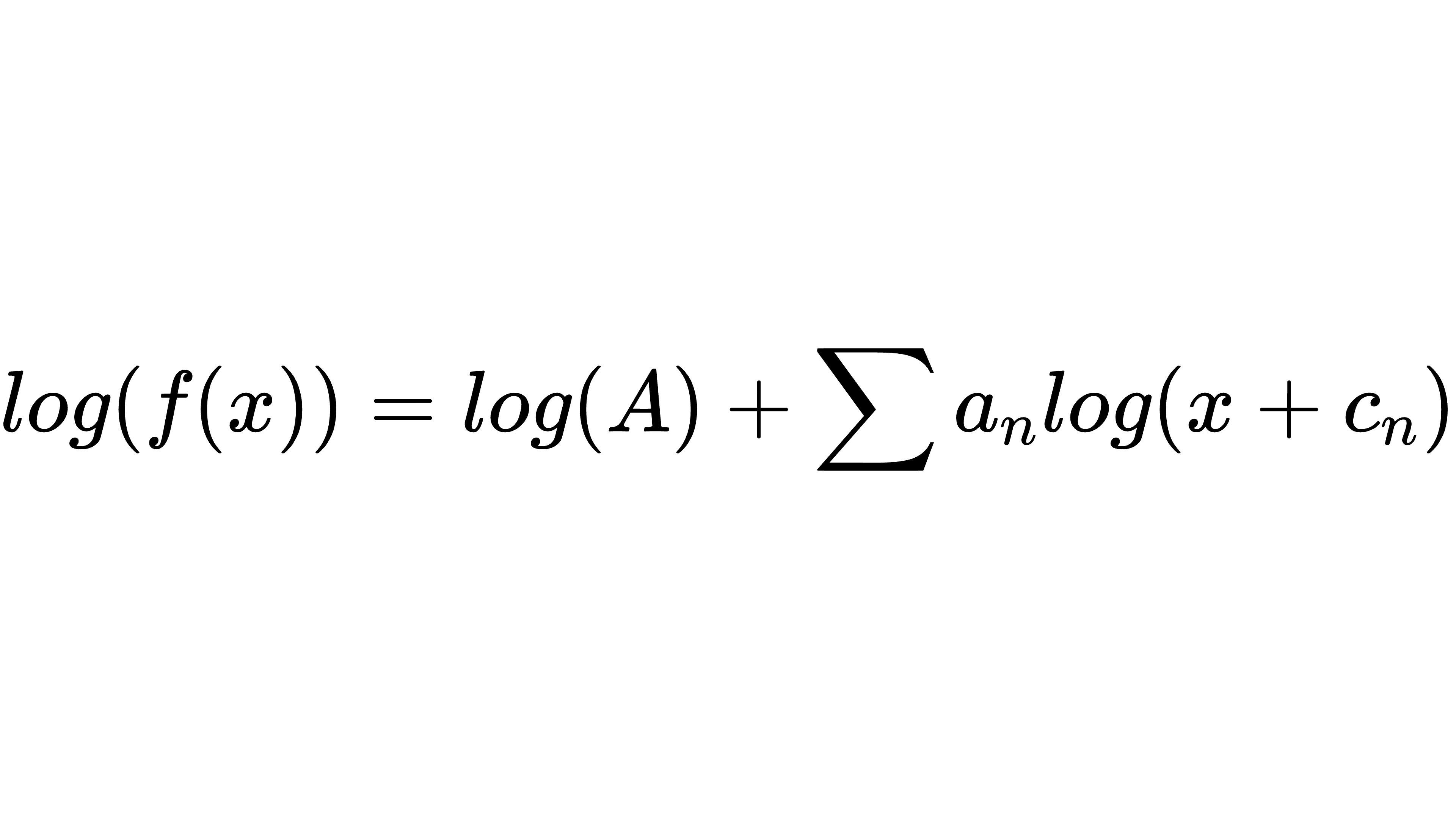
在绘制波德相位图时直接使用了上述的概念。增益图的绘制时则是以此概念为基础,因为每个极点或零点其增益的对数均从0开始,而且其渐近线只有一个转折点,因此绘制时可以再作简化。
直线近似的增益图
波德图增益分贝值一般都利用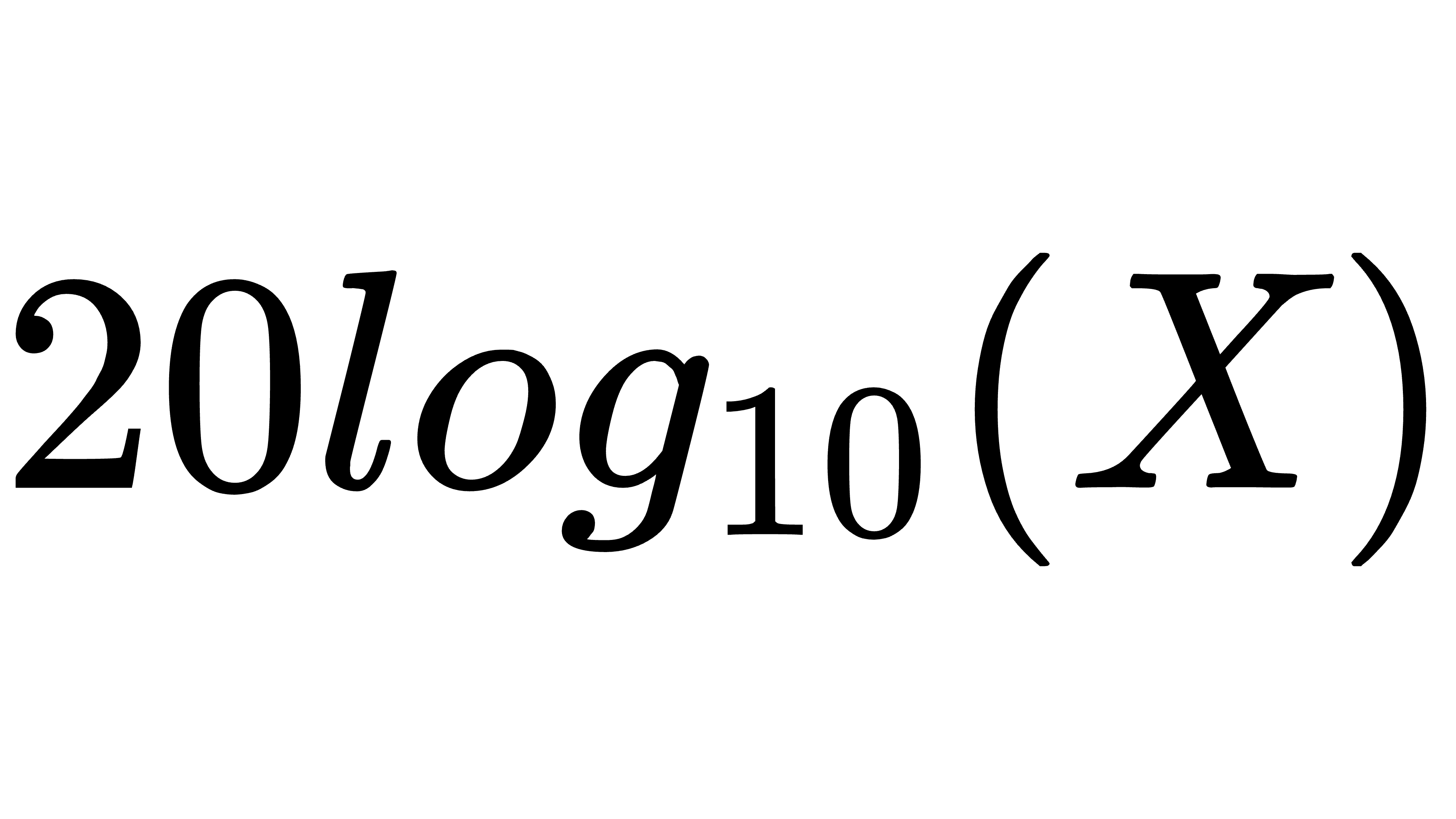
的公式。考虑以下的转换函数：
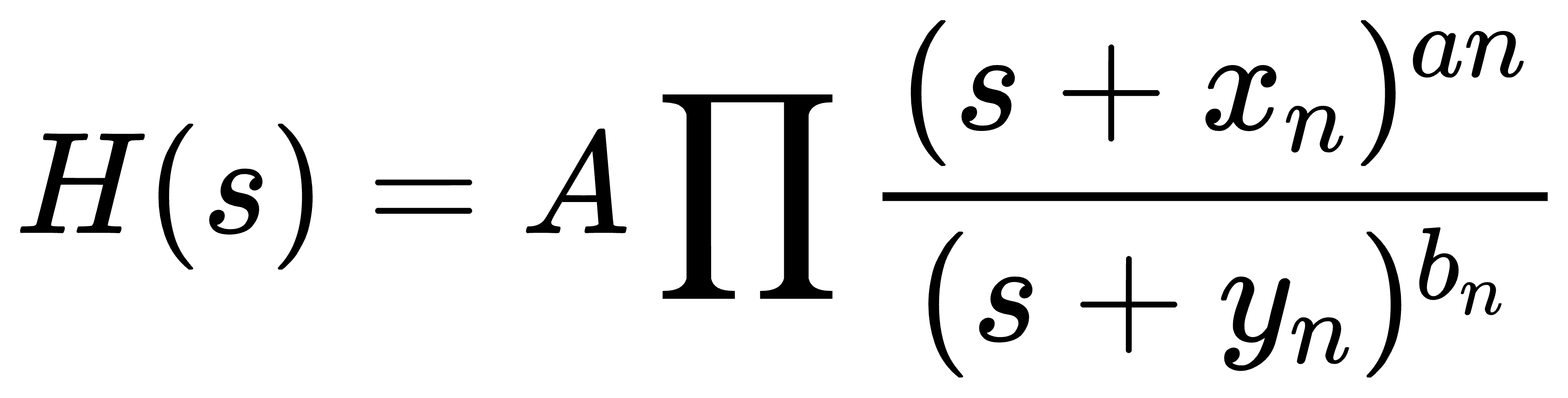
其中xn,yn 是常数, s=j
,an,bn>0, 而H是转换函数。
1)在每个对应 = xn (零点)的位置,将直线的斜率增加20an/dB 十倍频
2)在每个对应 = yn (极点)的位置,将直线的斜率减少20bn/dB 十倍频
3)图在起始点时的增益值,可以依照图中的角频率下限,计算其对应的 |H(j)|
4)图在起始点时的斜率则依照有多少零点及极点低于角频率下限,再依上述二个方式计算斜率,若所有点及极点均高于角频率下限,起始点时的斜率为零。
在系统稳定性的应用
波德图可用来计算负反馈系统的增益裕度(gain margin)及相位裕度,进而确认系统的稳定性。先定义以下的符号：
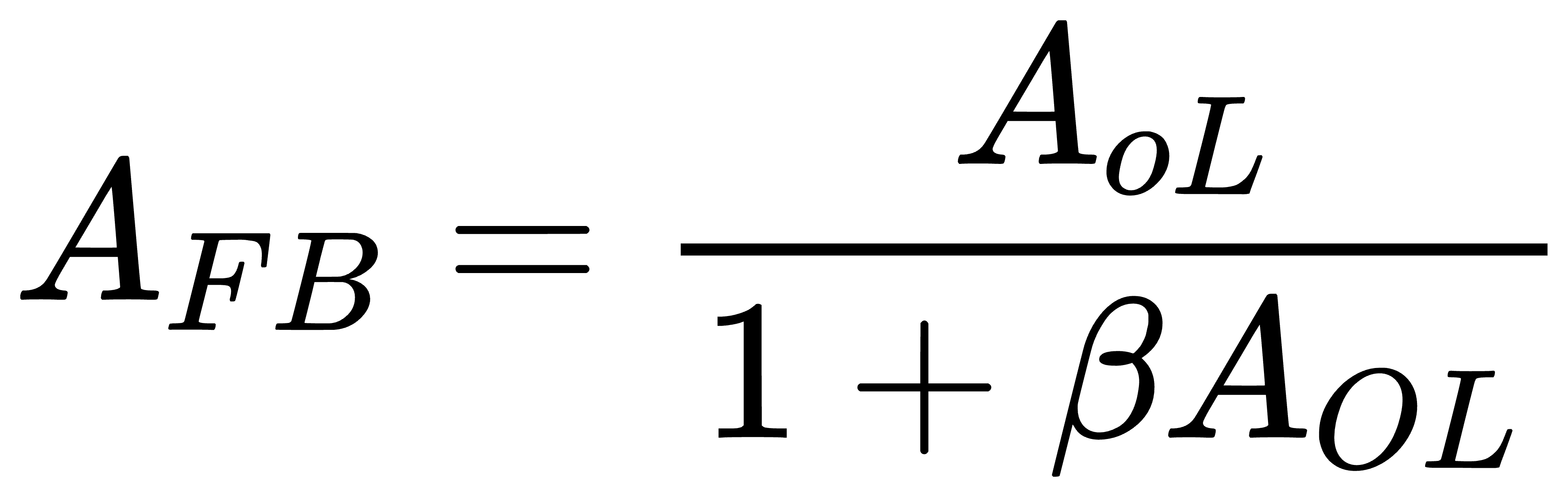
其中, A{FB} 是考虑反馈时的放大器增益(闭环增益),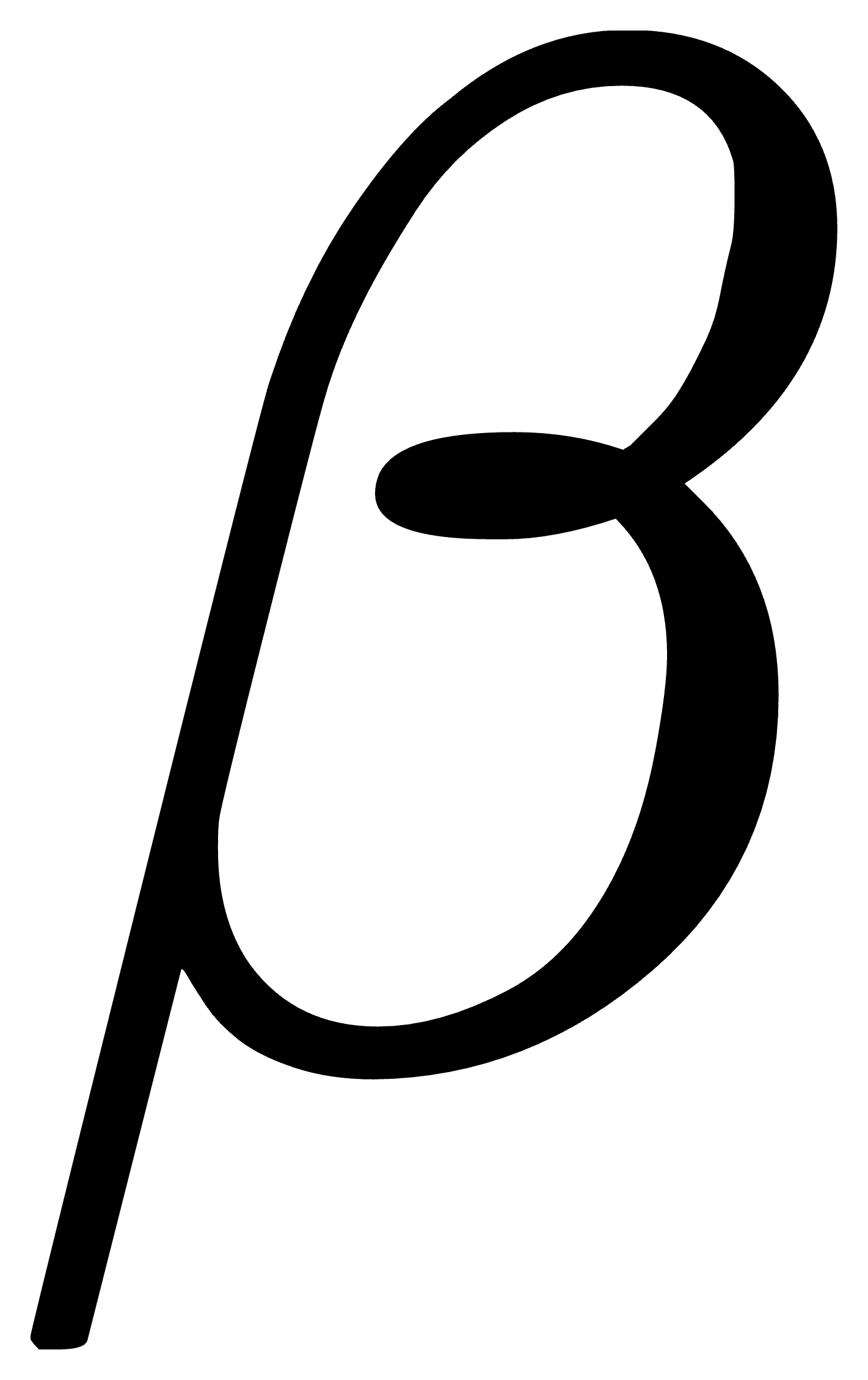
是反馈系数, A{OL} 是不考虑反馈时的放大器增益(开环增益)
在开环增益 A{OL}远大于1时,闭环增益A{FB} 可以用以下方式近似
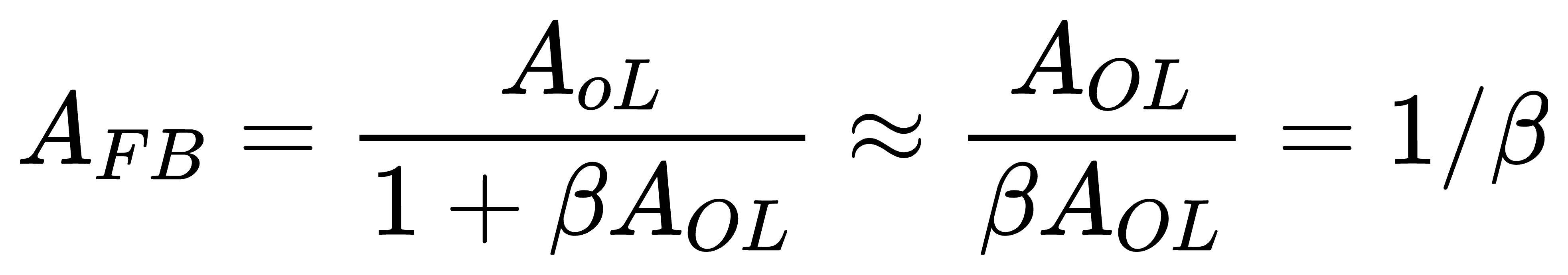
在开环增益 A{OL} 远小于1时,闭环增益 A{FB} 可以用以下方式近似
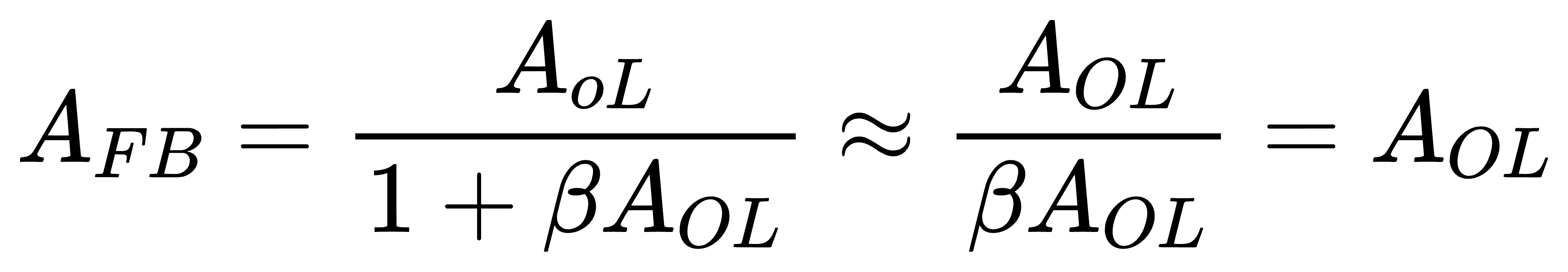
增益 A_{OL} 是频率的复变函数,有大小及相位。
上述的式子中,若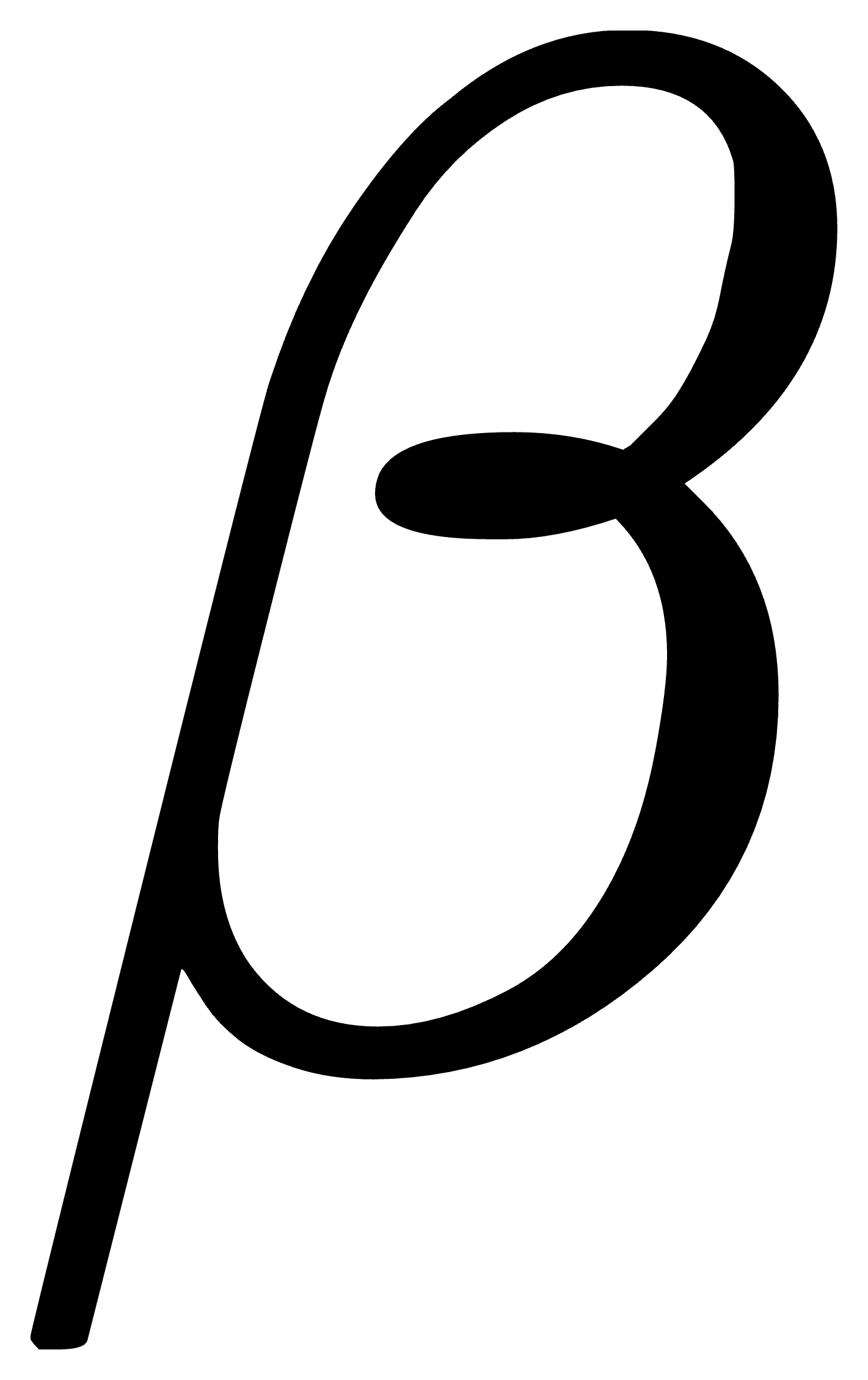 A_{OL} 乘积=−1时,可能会出现增益无穷大(即为不稳定)的情形。(若用大小和相位来表示,此时A的大小为1,相位为-180度,此条件即称为巴克豪森稳定性准则。配合波德图,不但可以判断系统是否稳定,也可以判断系统接近以上不稳定条件的程度。
系统的稳定性及稳态裕度
稳定是控制系统的重要性能, 也是系统能够正常运行的首要条件。对于设计人员来说, 花费大量精力的重点在于测量系统有多稳定, 或者准确地说在于测量系统所拥有的稳定性裕度有多大。无论是在工程应用中, 还是在理论研究上, 这里推荐大家使用相位裕度 (Phase Margin, PM) 和增益裕度 (Gain Margin, GM) 来作为系统稳定程度的度量。 这是因为：
① PM 和 GM 是系统稳定性最直观的量度；
② 开环设计法是数字的, 适合于计算机；
③ 这种方法不需要对控制系统进行任何的简化性假设。
如果控制系统结构如下图所示,断开反馈回路, 得到该系统开环传递函数的对数频率特性曲线如图右所示,图中, 相位裕度 (PM) (通常也称为相角裕度) 定义为 180°加开环幅相曲线幅值为 1 时的相位：
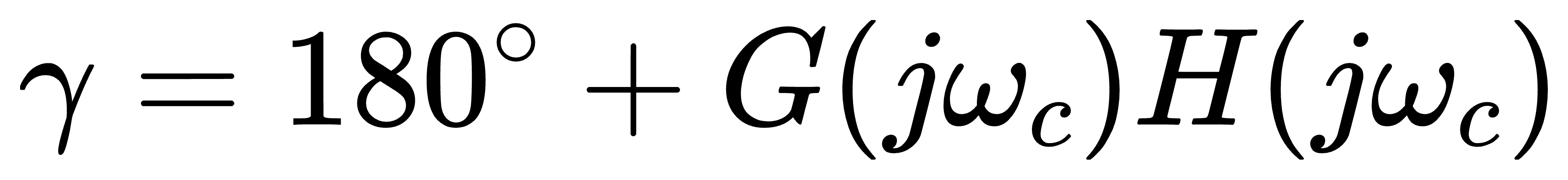
式中 ωc———系统的截止角频率。
增益裕度 (GM, 通常也称为幅值裕度) 定义为幅相曲线上, 相位为 - 180°时对应幅值的倒数：
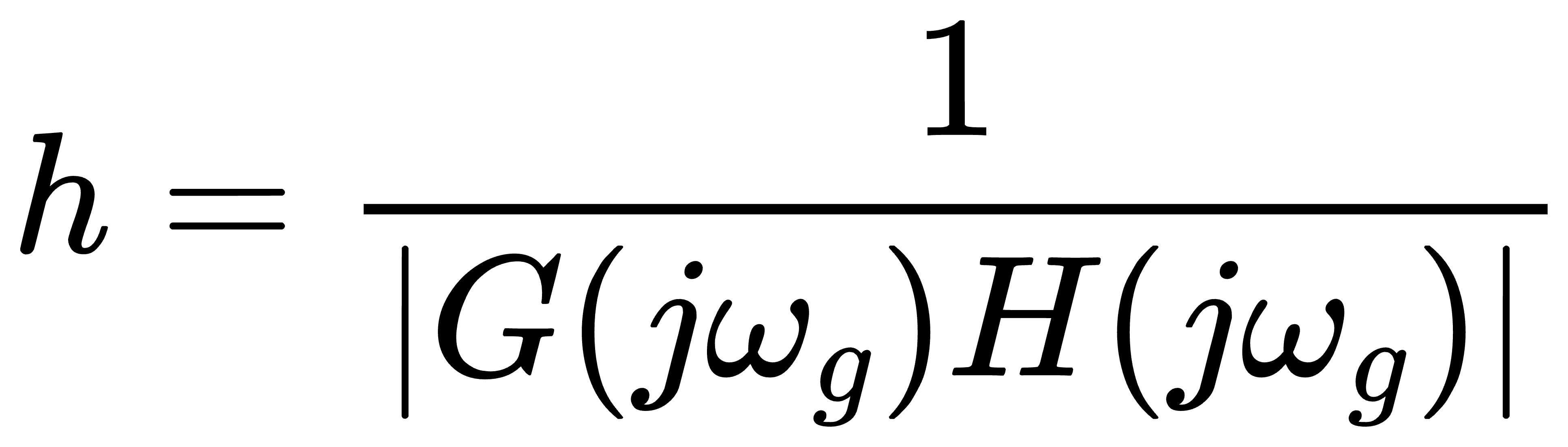
式中 ωg———相角交界角频率。 通常幅值裕度用分贝值 dB 表示, 上式可修改写为：
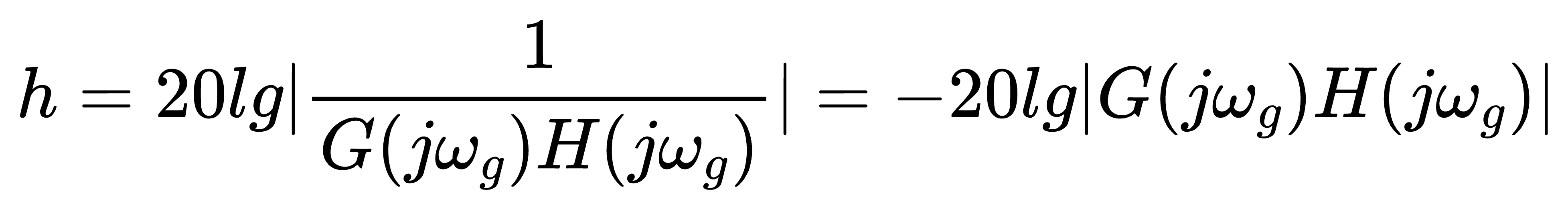
虽然目标是测量 PM和 GM的值,但是确定这两个量度的期望值需要判断。其原因之一是裕度大小随应用要求的变化而变化。例如,有些必须跟随指令信号,如阶跃指令信号的场合,除了极稳定的系统外都会产生超调。相对于响应变化柔和的指令信号来说,这样的应用需要更高的稳定裕度。此外,与其他应用相比,有些应用可以承受更大的超调量。最后,对于同样的响应,有些控制方法需要比其他方法更大的相位裕度或者增益裕度。例如,对于一个阶跃响应来说, 要获得相同的超调量, PI 调节器需要一定的相位裕度, 而对于 PID 调节器来说, 较小的相位裕度就可能消除所有超调。 经验表明, 增益裕度 (GM) 应为 10 ～ 25dB, 而相位裕度 (PM) 应为 35° ～ 80°, 这取决于具体应用及控制器类型。 一般情况下, 幅值裕度越大越好, 同样, 相角裕度也是越大越好。
参考内容
[1] 维基百科——伯德图
[2] 《交流伺服系统设计指南》——孙宇等编著
