• 前言
• Numpy
  • ndarray 对象
• SciPy
  • 优化——optimize
    • 最小二乘拟合
• pandas
  • Series
• 类函数的编写
• 处理矩阵经常用到的
  • 利用行列向量生成对角阵
• 获取xml中的数据

    * [xml中节点包含的属性：](#xml中节点包含的属性)
    * [节点类型](#节点类型)
    * [python获取xml节点：](#python获取xml节点)
        * [打印标签对之间的数据](#打印标签对之间的数据)
  

• 正则匹配
  • 正则表达式
    • re.compile 函数
• 其他
  • 动态生成变量名
• 小技巧
• 参考

前言

用python有近一年多的时间了,但水平还是很差,闲来无事,记录一些自己感觉有用的东西,仅此而已。

Numpy

ndarray 对象

可以通过给 array()函数传递 Python 的序列 对象来创建数组。数组的形状可以通过其shape 属性获得,它是一个描述数组各个轴长度的元组(tuple)。当设置某个轴的元素个数为-1 时,将自动计算此轴的长度。使用数组的 reshape()方法,可以创建指定形状的新数组,而原数组的形状保持不变。zeros()、ones()、empty()可以创建指定形状和类型的数组。其中：empty()仅仅分配数组所使用的内存,不对数组元素进行初始化操作,因此它的运行速度是最快的。

fromfunction()的第一个参数为计算每个数组元素的函数,第二个参数指定数组的形状。如生成9*9的乘法序列：

def fun(i,j):
    return (i+1) * (j+1)
print(np.fromfunction(fun, (9,9)))

关于切片,感觉还是利用形象的记忆比较有效,如下图所示

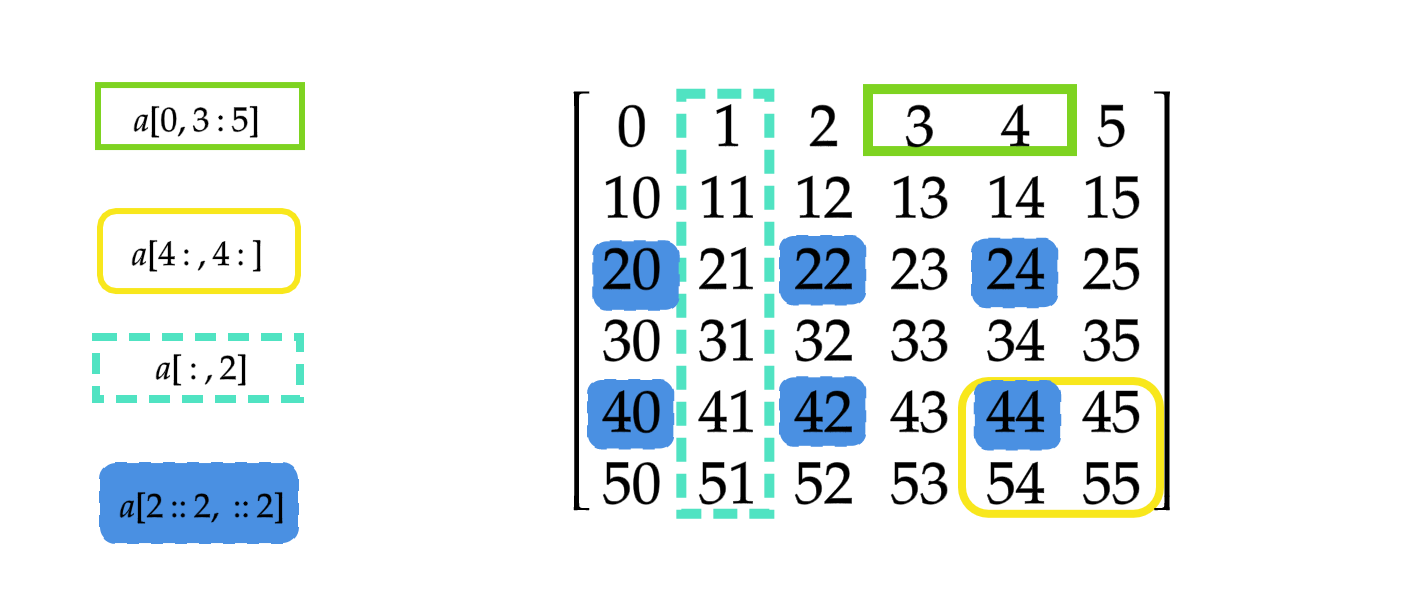
标准Python 中有比 for 循环更快的方案——使用列表推导式。但是列表推导式将产生一个新的列表,而不是直接修改原来列表中的元素。如

x = [math.sin(t) for t in x]

SciPy

SciPy在NumPy的基础上增加了众多的数学、科学以及工程计算中常用的模块,例如线性代数、常微分方程数值求解、信号处理、图像处理、稀疏矩阵,等等。

优化——optimize

最小二乘拟合

最小二乘是自己做参数辨识中最常用的一种方法了,假设有一组实验数据(xi , yi),我们事先知道它们之间应该满足某函数关系yi=f(xi),通过这些已知信息,需要确定函数f的一些参数。例如,如果函数f是线性函数 f(x)=kx+b,那么参数 k和b 就是需要确定的值。如果用p表示函数中需要确定的参数,那么目标就是找到一组p,使得下面的函数S的值最小：

这种算法被称为最小二乘拟合(Least-square fitting)。在optimize 模块中,可以使用leastsq()对数据进行最小二乘拟合计算。

pandas

虽然pandas采用了大量的NumPy编码风格,但二者最大的不同是pandas是专门为处理表格和混杂 数据设计的。而NumPy更适合处理统一的数值数组数据。

默认使用使用下面的方式引入pandas:

import pandas as pd

因为Series和DataFrame用的次数非常 多,所以将其引入本地命名空间中会更方便：

from pandas import Series, DataFrame 

要使用pandas,你首先就得熟悉它的两个主要数据结构：Series和DataFrame。

Series

Series是一种类似于一维数组的对象,它由一组数据(各种NumPy数据类型)以及一组与之相关 的数据标签(即索引)组成。仅由一组数据即可产生最简单的Series：

obj = pd.Series([4, 7, -5, 3])

Series的字符串表现形式为：索引在左边,值在右边。由于没有为数据指定索引,于是会自动创建一个0到N-1(N为数据的长度)的整数型索引。可以通过Series 的values和index属性获取其数组表示形式和索引对象：

obj.values

可以通过Series带有可以对各个数据点进行标记的索引：

obj = pd.Series([4, 7, -5, 3], index=['d', 'b', 'a', 'c'])

这样就可以通过索引的方式选取Series中的单个或一组值, 如：

obj['a']

如果数据被存放在一个python字典中,也可以直接通过这个字典来创建Series：

data = {'Ohio': 35000, 'Texas': 71000, 'Oregon': 16000, 'Utah': 5000}
obj = pd.Series(sdata)

对于许多应用而言,Series最重要的一个功能是,它会根据运算的索引标签自动对齐数据。

类函数的编写

已自己写的简单的串联机器人的运动学为例,

class robot:
    def __init__(self,theta0,alpha,a,d,beta,tool):
        self.theta0 = deg2Rad(np.array(theta0))  #这里引入了其他地方写的函数,不过非常简单,就是将输入角度变成弧度
        self.alpha = deg2Rad(np.array(alpha))
        self.a = np.array(a)
        self.d = np.array(d)
        self.beta = deg2Rad(np.array(beta))
        self.position = []
        self.pose = []
        self.Jacobian = []
        self.tool =np.array([[1,0,0,tool[0]],[0,1,0,tool[1]],[0,0,1,tool[2]],[0,0,0,1]])
        np.set_printoptions(suppress=True)

    def FK(self,th):
        # 这里theta 的格式为 N*6, 方便一次性处理
        th = np.array(th).reshape(-1,6)   #主要是担心输入形式为 [0,0,0,0,0,0] 这种格式的
        th = deg2Rad(th)
        alpha = self.alpha
        a = self.a
        d = self.d
        beta = self.beta
        #上面这样写不写,都是无所谓的,追求效率的话,这些代码有很多地方可以优化,不过对于自己处理一些文件,足以。
        axis_z = np.array([0,0,1])
        T0j = []
        T0j.append(np.eye(4))
        for theta in th:
            theta = np.array(theta) + self.theta0    #以零点作为基准
            T = np.eye(4)
            for i in range(6):
                cth = np.cos(theta[i])
                sth = np.sin(theta[i])
                ca = np.cos(alpha[i])
                sa = np.sin(alpha[i])
                cb = np.cos(beta[i])
                sb = np.sin(beta[i])
                tans =  np.array(   [[cth, -sth * ca, sth * sa, a[i] * cth],
                                     [sth, cth * ca, -cth * sa, a[i] * sth],
                                     [0,   sa,       ca,        d[i]],
                                     [0,   0,         0,         1]])
                rotBeta = np.array([[cb, 0, sb, 0],
                                    [0, 1, 0, 0],
                                    [-sb, 0, cb, 0],
                                    [0, 0, 0, 1]])					#标准的DH参数里面,没有用到beta参数,即绕Y轴旋转的,根据标定的结果为准。
                A =  np.dot(tans, rotBeta)
                T = np.dot(T,A)
                T0j.append(T)

            T0t = np.dot(T,self.tool)
            self.position.append(T0t[:3,3])
            # 求解雅克比矩阵,雅克比矩阵能用到的地方太多了,也太重要了。
            J = []
            for i in range(6):
                vec_Z = np.dot(T0j[i][:3,:3],axis_z)
                Tjt = np.dot(np.linalg.inv(T0j[i]),T0t)
                vec_P = np.dot(T0j[i][:3,:3],Tjt[:3,3])
                J.append(np.cross(vec_Z,vec_P))
            self.Jacobian.append(np.array(J).transpose())

调用的话,就比较简单了：

dhPar = np.array([[ 0,        154,             0,         -90,           0],
                 [-90,          0,       418.865,           0,           0],
                 [  0,          0,       387.265,           0,           0],
                 [ 90,    144.421,             0,          90,           0],
                 [  0,    122.213,             0,          90,           0],
                 [  0,      107.5,             0,           0,           0]])
                 #输入标定里面的结果
theta0 = [0,0,0,0,0,0]  # 根据具体的标定,去选择修正。 
theta0 = dhPar[:,0] - np.array(theta0)
d = dhPar[:,1]
a = dhPar[:,2]
alpha = dhPar[:,3]
beta =  dhPar[:,4]
toolOffset=[44.927,-21.859,62.138]   					 #工具坐标系
yourRobot = robot(theta0,alpha,a,d,beta,toolOffset) 	 #实例的时候,就会初始化给那些成员函数,和C++非常相似


thetaTest = [[-18.417,22.954,97.427,-125.640,108.328,-87.907]]  #可以写入 N*6 行的关节角,方便一次性在函数体内进行计算
ECR5.FK(thetaTest)                                              #通过正解,可以算出很多结果。
print(ECR5.position)											#输出结果,或者是将结果做下一部的转化、或给其他函数做输入等等。

处理矩阵经常用到的

利用行列向量生成对角阵

这个问题的引入是在自己做辨识的时候用上的,需要将力矩向量变成对角矩阵,然后进行辨识。

大致有三种方法,np.array + np.diag,np.array + np.identity,np.matrix + np.diagflat。其中最快的属于第一种,下面给出第一种的使用：

tau = np.array(tau)
for i in range(len(tau))
	tor = np.diag(tau[i])

矩阵的合并

矩阵合并用的最多的是np.append, 比如np.append(m1,m2,axis = 0) 表示合并列,和matlab [a;b], 很相似,类似的,np.append(m1,m2,axis=1)和 matlab [a,b] 类似,为列合并。

获取xml中的数据

这个是为了方便自己在读取DH参数的时候用到的。

xml中节点包含的属性：

1, nodeName——节点名称
2, nodeValue——节点值
3, nodeType——节点类型
   nodeType为1说明是元素节点,nodeType为2说明是属性节点。

节点类型

1, 元素节点
2, 文本节点
3, 属性节点

python获取xml节点：

DH.xml文件 (简单的例子)

<?xml version="1.0" encoding="utf-8"?>
<Root>
    <DH>            
        <Axis1>
            <theta>0</theta>
            <d>154.0</d>
            <a>-0.631</a>
            <alpha>-90.045</alpha>
            <beta>0</beta>
        </Axis1>       
    </DH>
</Root>

代码：

import lsqyRobot as lR
from xml.dom import minidom

xmlFile = lR.askFileWhere()
dom=minidom.parse(xmlFile)
root=dom.documentElement       #获取dom对象元素
print(root.nodeName)
print(root.nodeValue)
print(root.nodeType)

其中 askFilewhere() 在 lsqyRobot.py (为方便自己写的函数包)代码如下

def askFileWhere():
    root = tk.Tk()
    root.withdraw()
    file_path = filedialog.askopenfilename()
    return file_path

运行结果如下

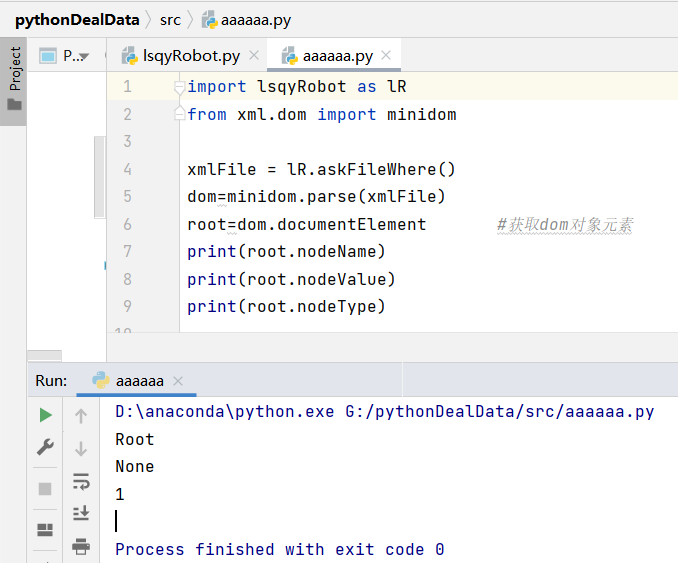
这里如果想在打开文件的时候给予提示,可将 askFileWhere()改写为：

def askFileWhere(tit):
    root = tk.Tk()
    root.withdraw()
    file_path = filedialog.askopenfilename(title = "{}".format(tit))
    return file_path

打印标签对之间的数据

node.firstChild.data

代码如下：

import lsqyRobot as lR
from xml.dom import minidom

xmlFile = lR.askFileWhere()
dom=minidom.parse(xmlFile)
thetaValue = dom.getElementsByTagName("theta")
dValue= dom.getElementsByTagName("d")
aValue= dom.getElementsByTagName("a")
alphaValue = dom.getElementsByTagName("alpha")
betaValue = dom.getElementsByTagName("beta")

运行结果如下(调试状态,其实都可以看到值,感兴趣的自己去尝试下,并不难)

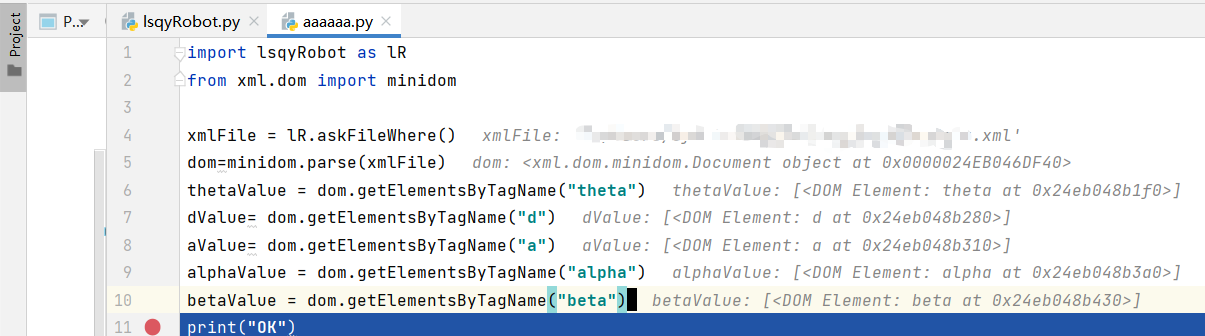
目前就记录到这,用到再记了。

正则匹配

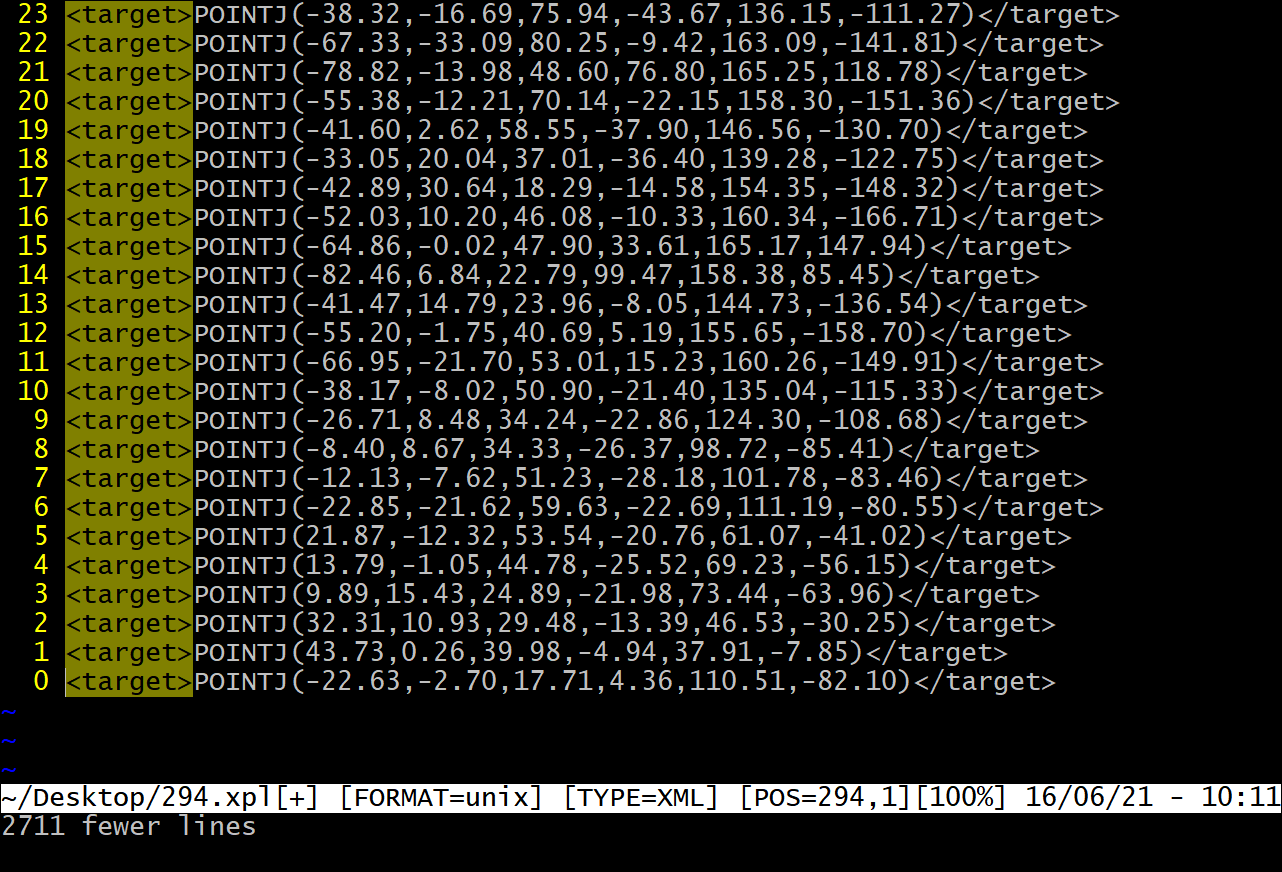
事情的起因是要筛选标定程序里的一些点的,由于在标定的时候,自动生成的点位(一般是朝着一个方向,即姿态不怎么发生变化),需要实际去跑这些点位,可有的时候自动生成的点位无法保证是安全的,这样就需要手动去调整,这个时候需要筛选出调整后的点位。比如最后调整好的文件可能是长成这样的：

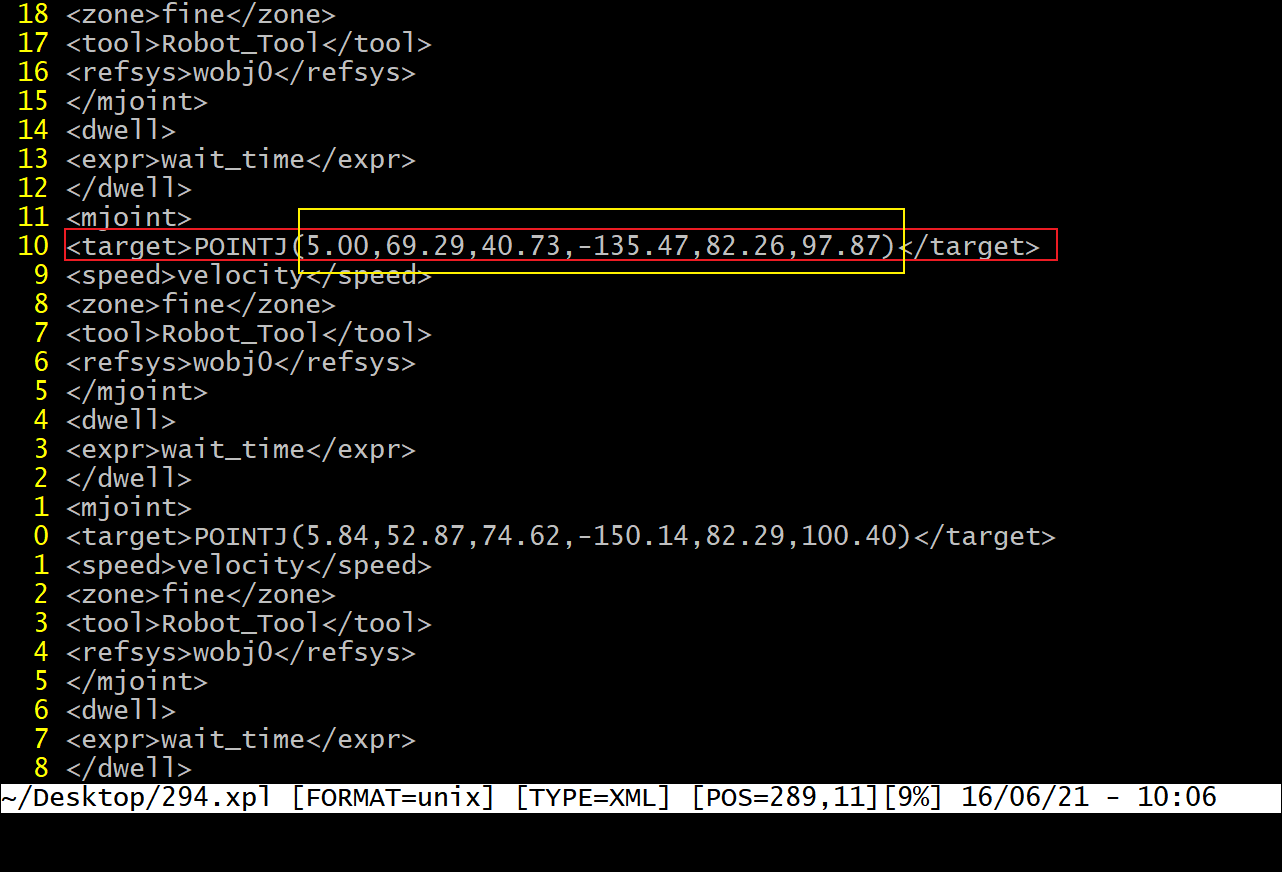
不过只需要里面的数字,就是画黄线那部分,还需要将,,变成Tab, 或者是\t,用 vim 的正则等可以非常快的(大概一分钟)就能解决这个问题, 第一步,除了选中部分,其他部分均删除：

:v /<target>/d

通过这一步就差不多把需要的给筛选出来了

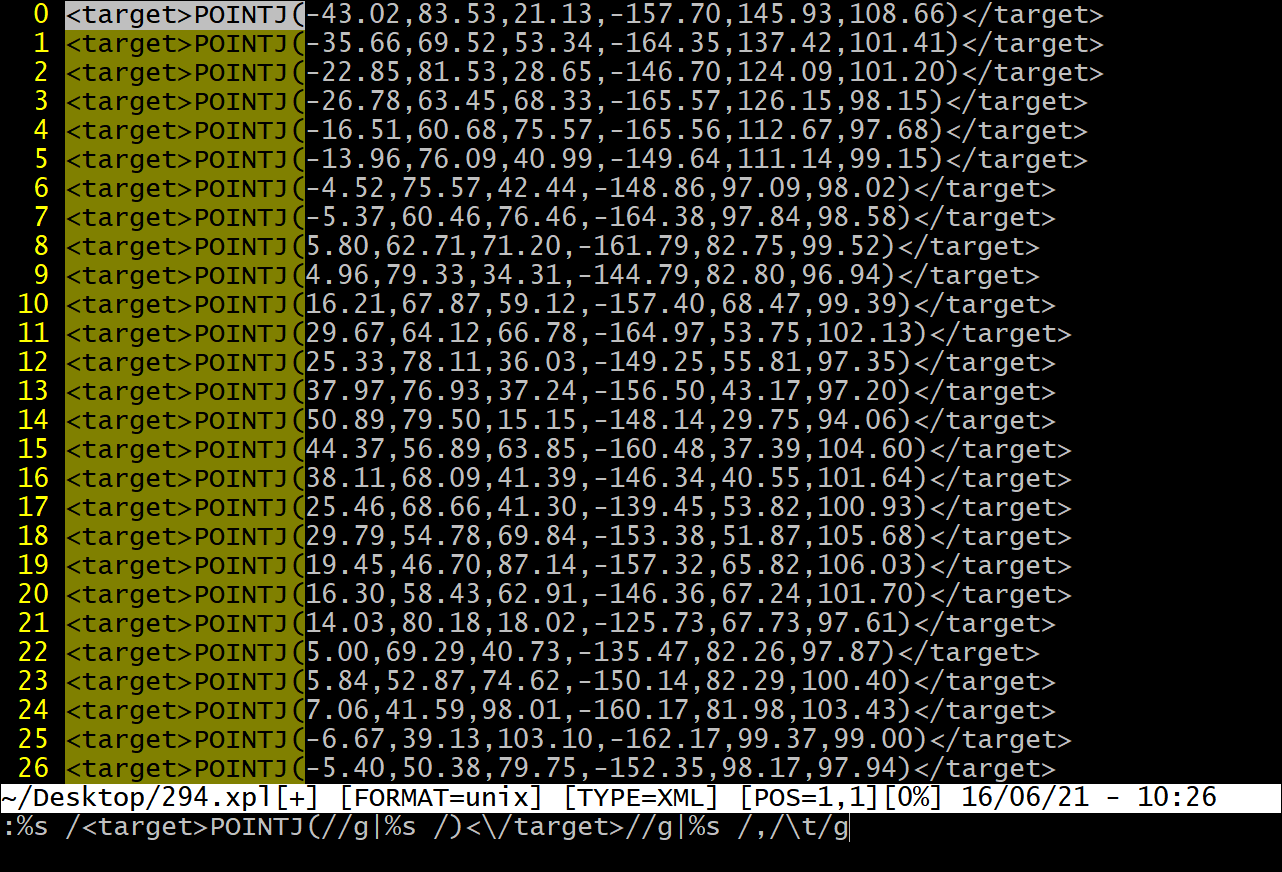
剩下的就是简单的vim正则替换了:

:%s /<target>POINTJ<//g|%s /)<\/target>//g|%s /,/\t/g

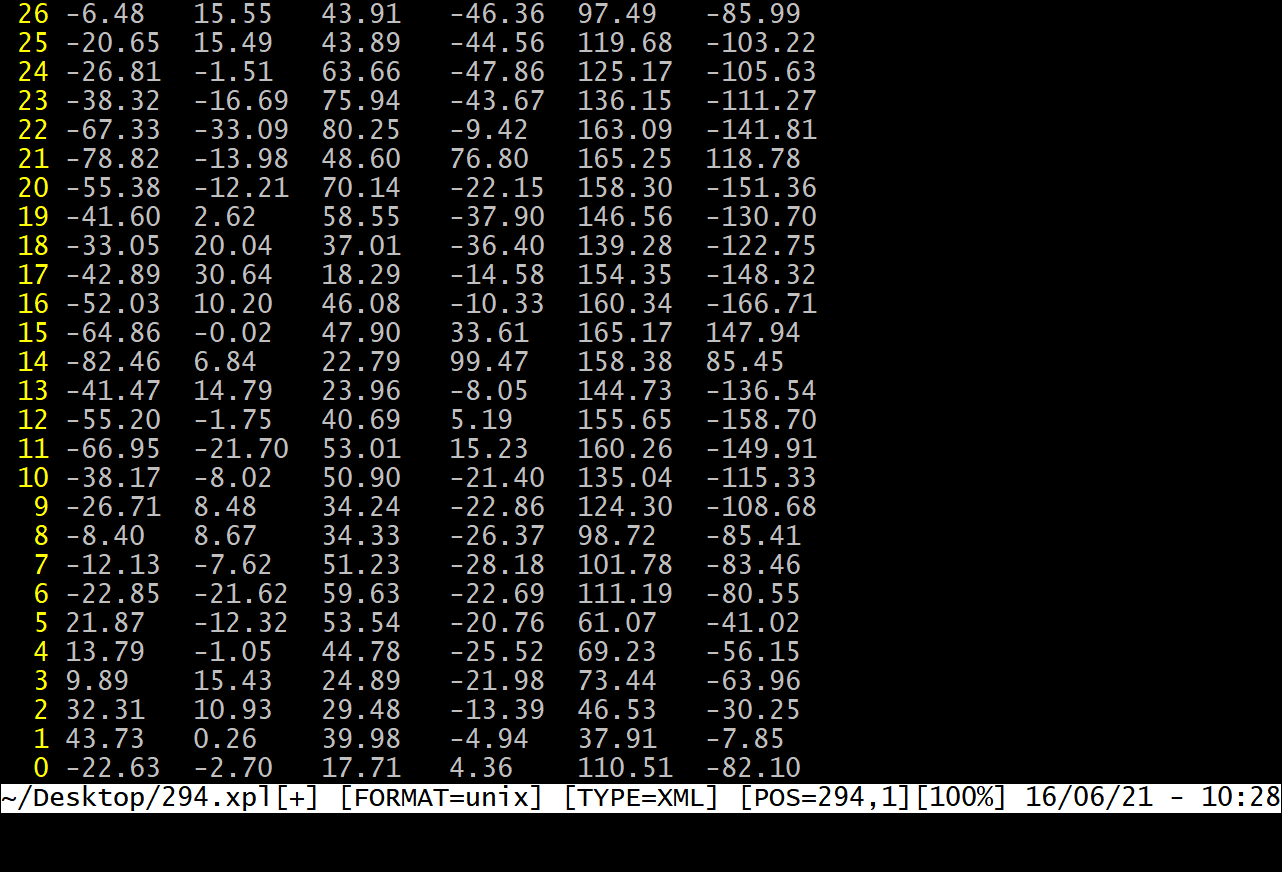
这个前提是对 vim 的正则替换有些熟悉,哪怕几百万行,替换的时间也是非常短的,当然,这种核心思想在于正则替换,使用python一样可以做。

正则表达式

正则表达式提供了一种灵活的在文本中搜索或匹配(通常比前者复杂)字符串模式的方式。正则表 达式,常称作regex,是根据正则表达式语言编写的字符串。Python内置的re模块负责对字符串应 用正则表达式。

re模块的函数可以分为三个大类：模式匹配、替换以及拆分。当然,它们之间是相辅相成的。一个 regex描述了需要在文本中定位的一个模式,它可以用于许多目的。

re.compile 函数

compile 函数用于编译正则表达式,生成一个正则表达式( Pattern )对象,供 match() 和 search() 这两个函数使用。语法格式为：

re.compile(pattern[, flags])
pattern : 一个字符串形式的正则表达式
flags : 可选,表示匹配模式,比如忽略大小写,多行模式等,具体参数为：
re.I 忽略大小写
re.L 表示特殊字符集 \w, \W, \b, \B, \s, \S 依赖于当前环境
re.M 多行模式
re.S 即为 . 并且包括换行符在内的任意字符(. 不包括换行符)
re.U 表示特殊字符集 \w, \W, \b, \B, \d, \D, \s, \S 依赖于 Unicode 字符属性数据库
re.X 为了增加可读性,忽略空格和 # 后面的注释

其他

动态生成变量名

在我的收藏夹吃灰了好久，收藏的具体原因给忘了，应该不怎么常用

如果你想生成v1,v2…v100这一百个变量，使用其他静态编译语言只能在代码中手动写出这100个变量名，但是在python中可以使用循环方便地动态生成。 python中有一个函数locals()，定义是：

locals(...)

    locals() -> dictionary

即返回当前作用域的所有变量, 所以可以用这个函数来创建变量

for i in range(4):
    name='v'+str(i)
    locals()['v'+str(i)]=i

print v1,v2,v3

小技巧

1, 在使用np.array的时候,默认是以科学计数法来显示的,在写机器人代码的时候与示教器上的数值进行核对时,会有些费事,使其正常显示可以设置为

np.set_printoptions(suppress=True)

2, 保存高清图像,指定 dpi 与设置bbox_inches=‘tight’,这里dpi越大,越清晰,当然,导出的时间也越慢。

plt.savefig('./yourPic.jpg',dpi=500,bbox_inches = 'tight')

参考

[1] 《python 科学计算》—— 张若愚等著

[2] 《利用 Python 进行数据分析》——Mckinney Wes

[3] 龟的小号

[4] (Python 动态生成变量名)(https://blog.csdn.net/Baoli1008/article/details/47980779)