在了解角速度这块的时候，有必要了解一些基础的知识；
反对称矩阵
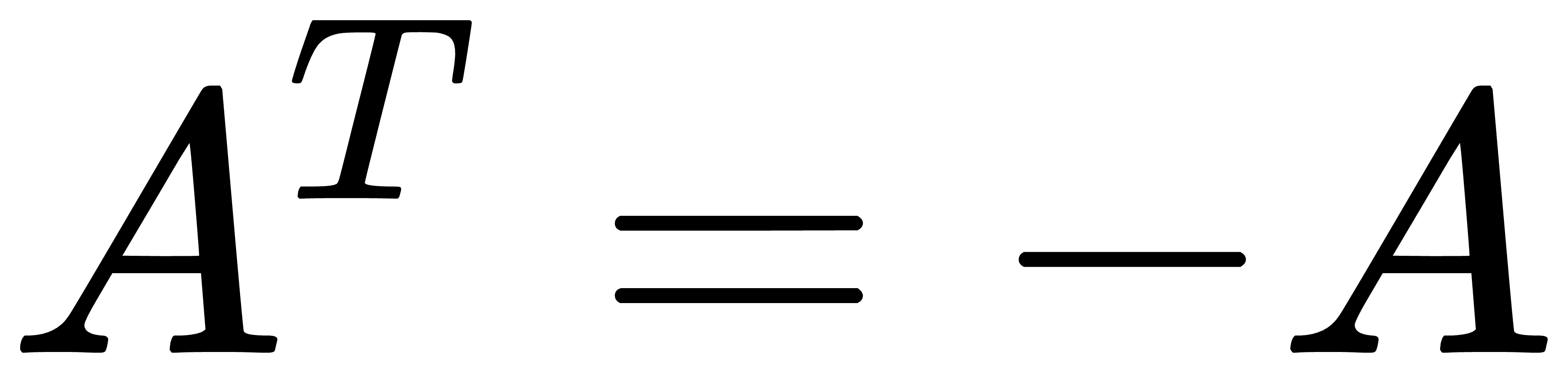
称其为反对称矩阵，将向量表示成反对称矩阵如下
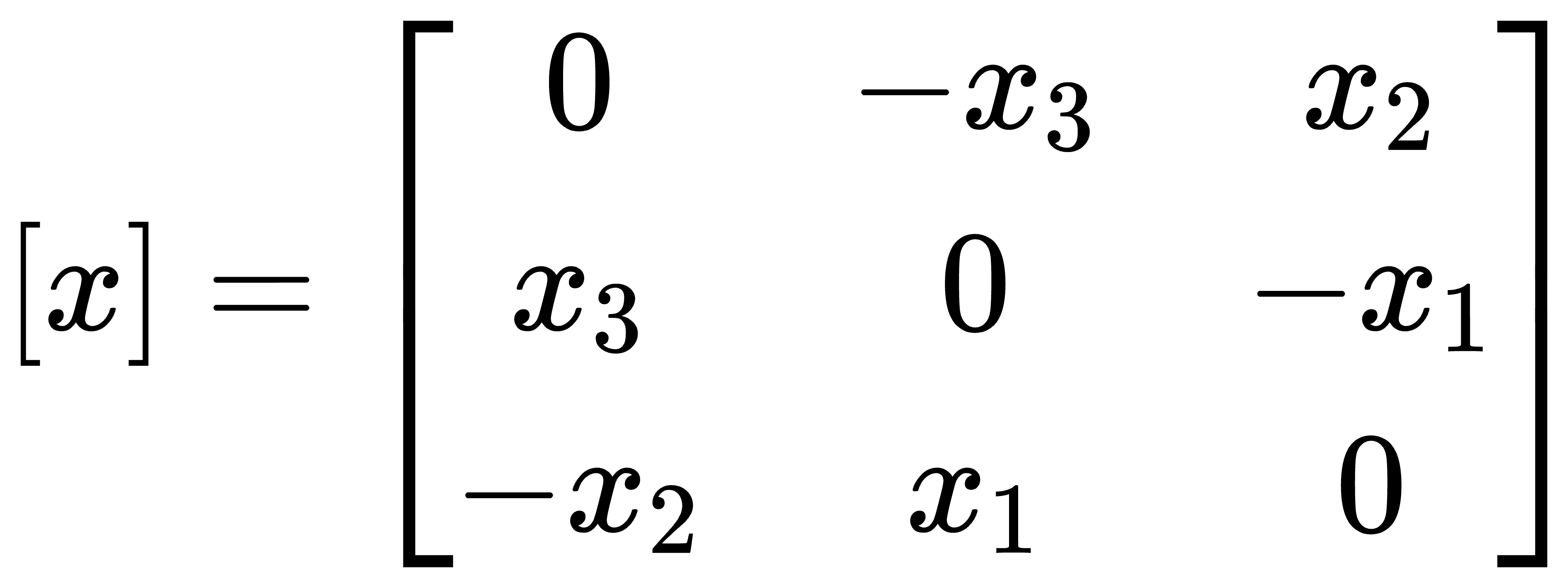
后面用符号[x]来表示向量x的反对称矩阵，将所有的3*3反对称矩阵称为so(3), 其中so表示反对称矩阵，定义如下
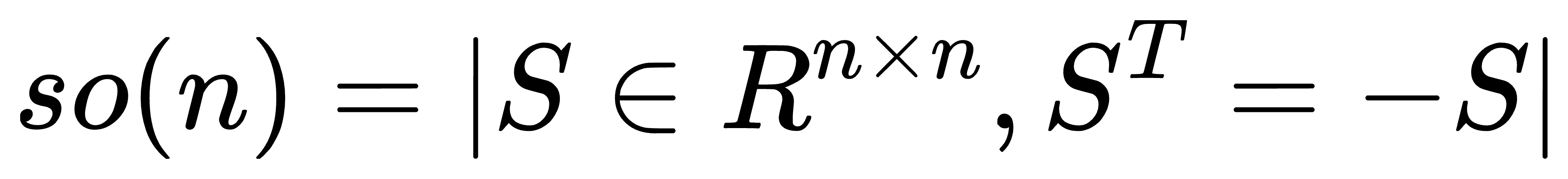
其中反对称矩阵so(3)称为SO(3)群的李代数，SO表示特殊正交（special orthogonal）的意思, 特殊在detR=+1,用于表示空间中的旋转矩阵，其SO的定义如下
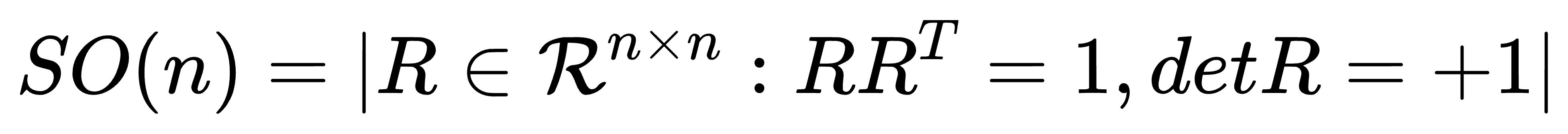
角速度表示
R可以表示空间中的旋转，那如果想知道空间旋转的角速度，是不是直接求导就行了？和他提出的疑问是一样的
当然不能直接求导，因为矩阵里面有9个变量，只希望用三个变量来表示角速度，我们知道，角速度可以通过一个旋转轴和对应的旋转速度来表示
空间角速度
这里假设了旋转轴为
, 是一个相对于惯性坐标系，也可以称之为静止坐标系，为了单位的统一，这里可以假设旋转轴为单位旋转向量，其中单位向量的识别符为在上面加个帽子，即
，用单位旋转轴乘以其速率，即可得到角速度向量 ,即
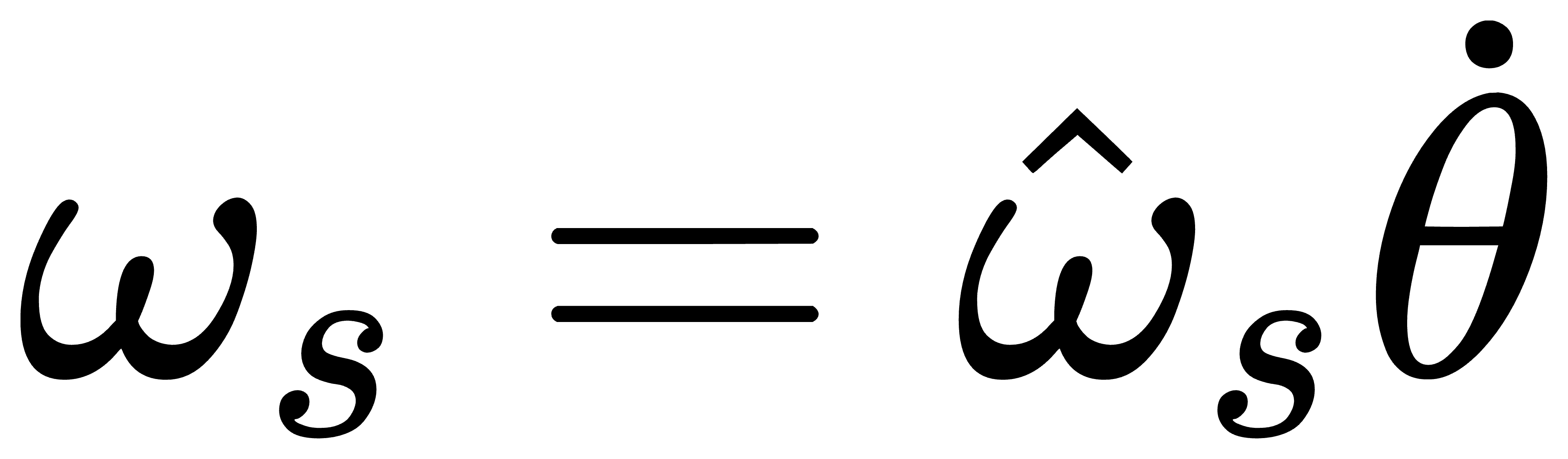
这样坐标系{b}在绕这个轴旋转时，其x轴方向将相对于s坐标系画一个圆，
不难得到，坐标系{b}的三个轴的速度可以表示为
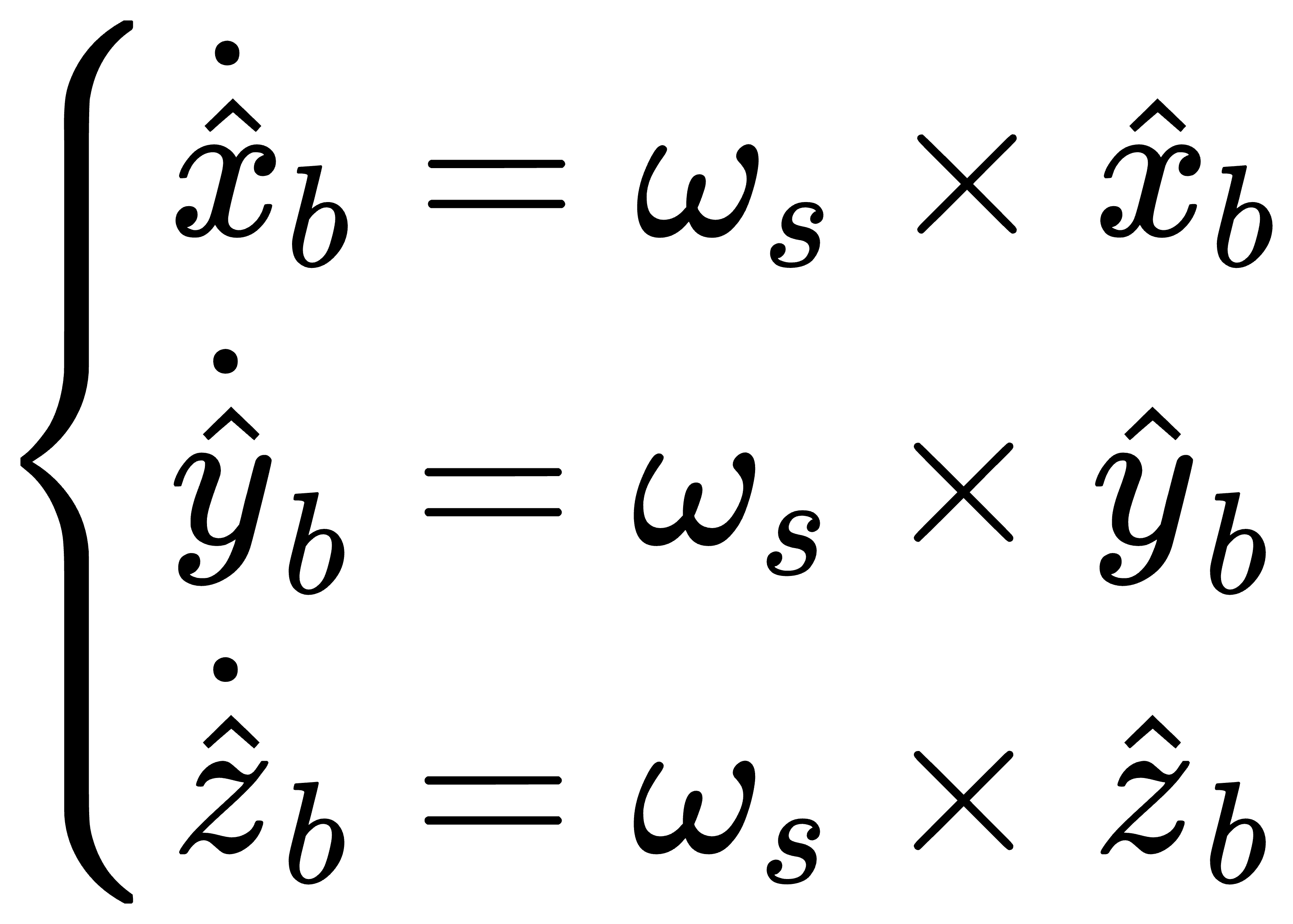
利用括号运算符（表示叉乘）， 通过上式，就可以直接得到如下关系式了（比直接看机器人操作的数学导论更容易理解，那书中就直接定义了，也没给出解释，搞得有点懵）
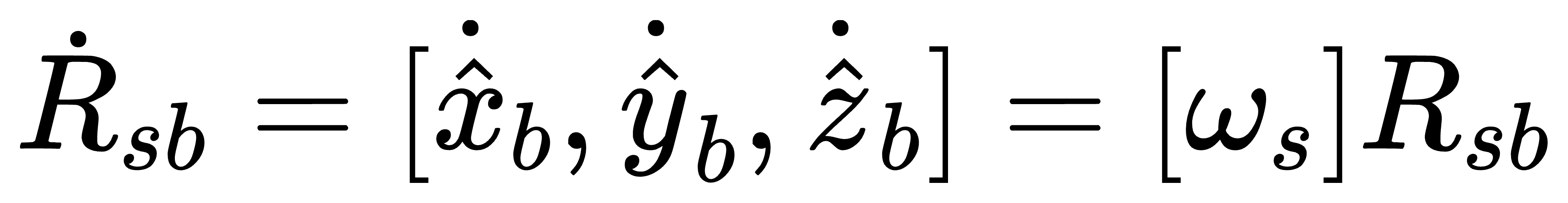
空间旋转轴的表示方法
相对于s坐标系的旋转矩阵一般可以省略下标，通过以上推导，就不难得到第一个重要的公式，即
当然，这里给出的角速度是相对于空间坐标系的，当然可以相对于物体坐标系，通过下标对消规则，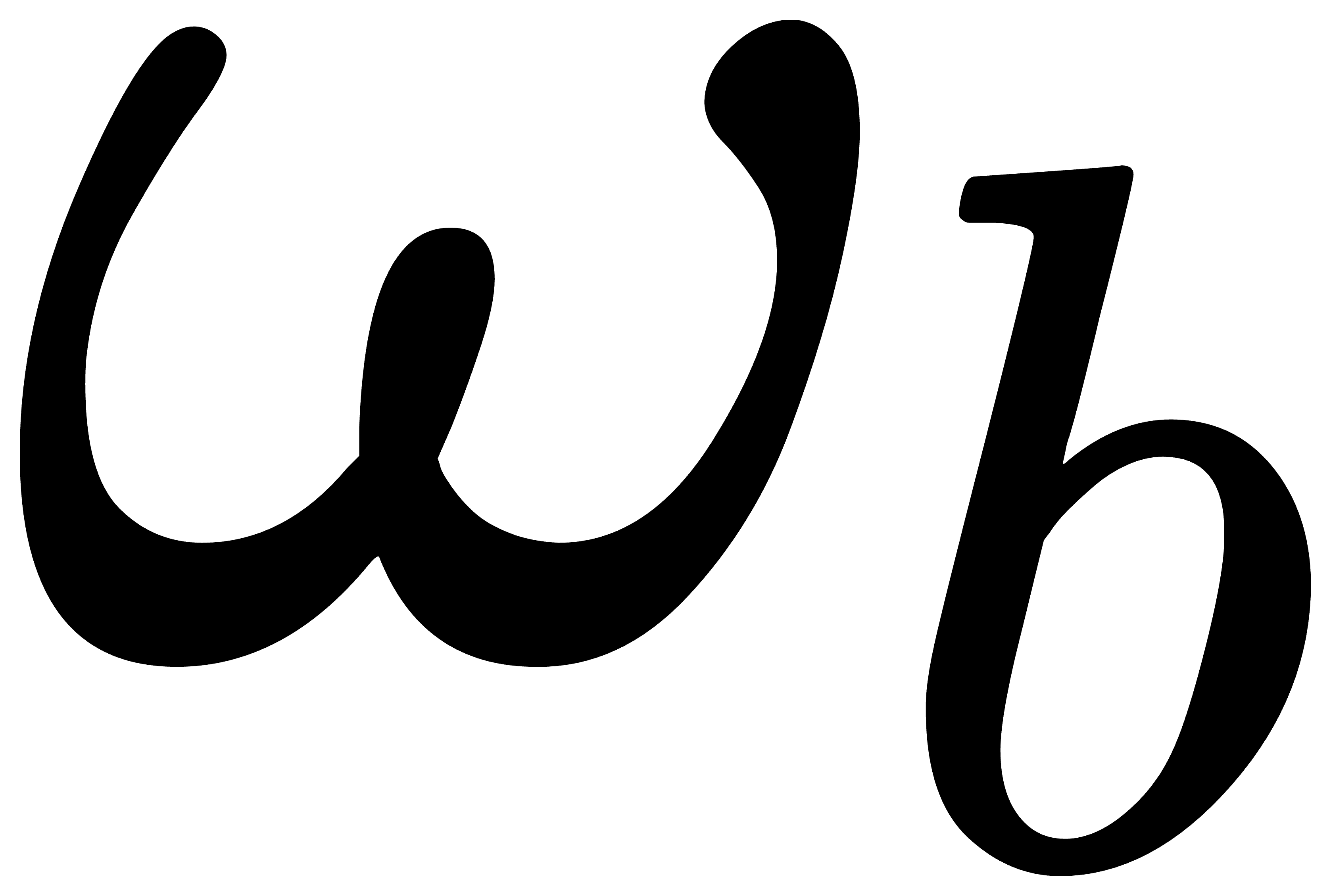
可以表示为
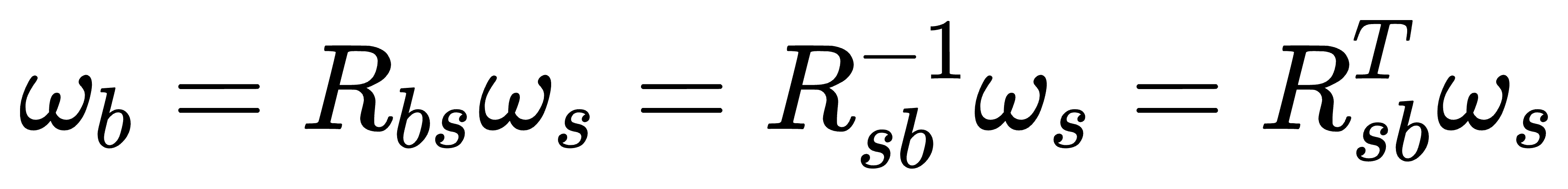
下面得到第二个重要公式前，需要知道一个定理，即
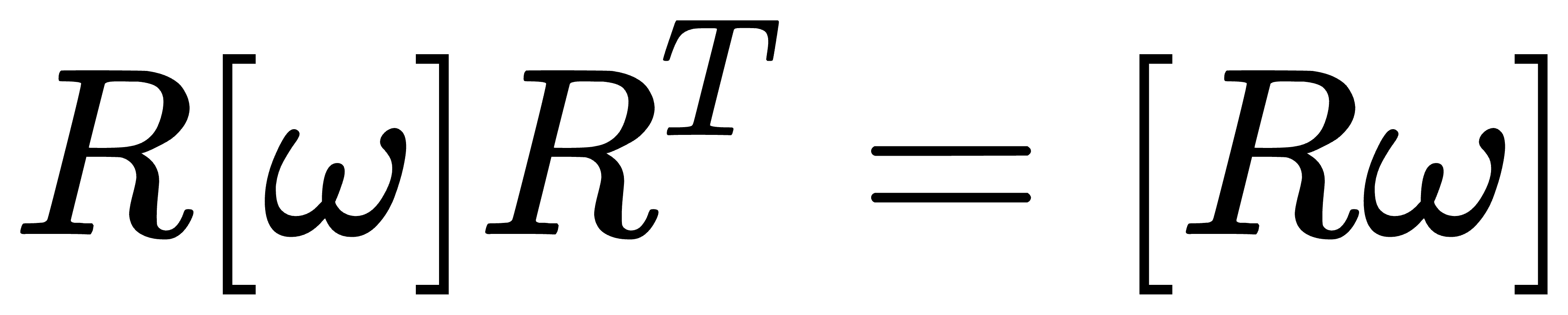
这样不难推导出第二个重要公式，即
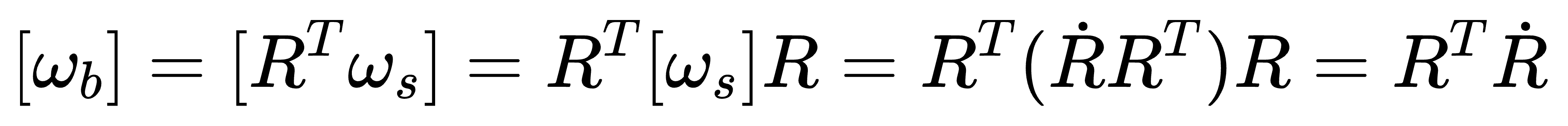
物体角速度的解释
值得注意的是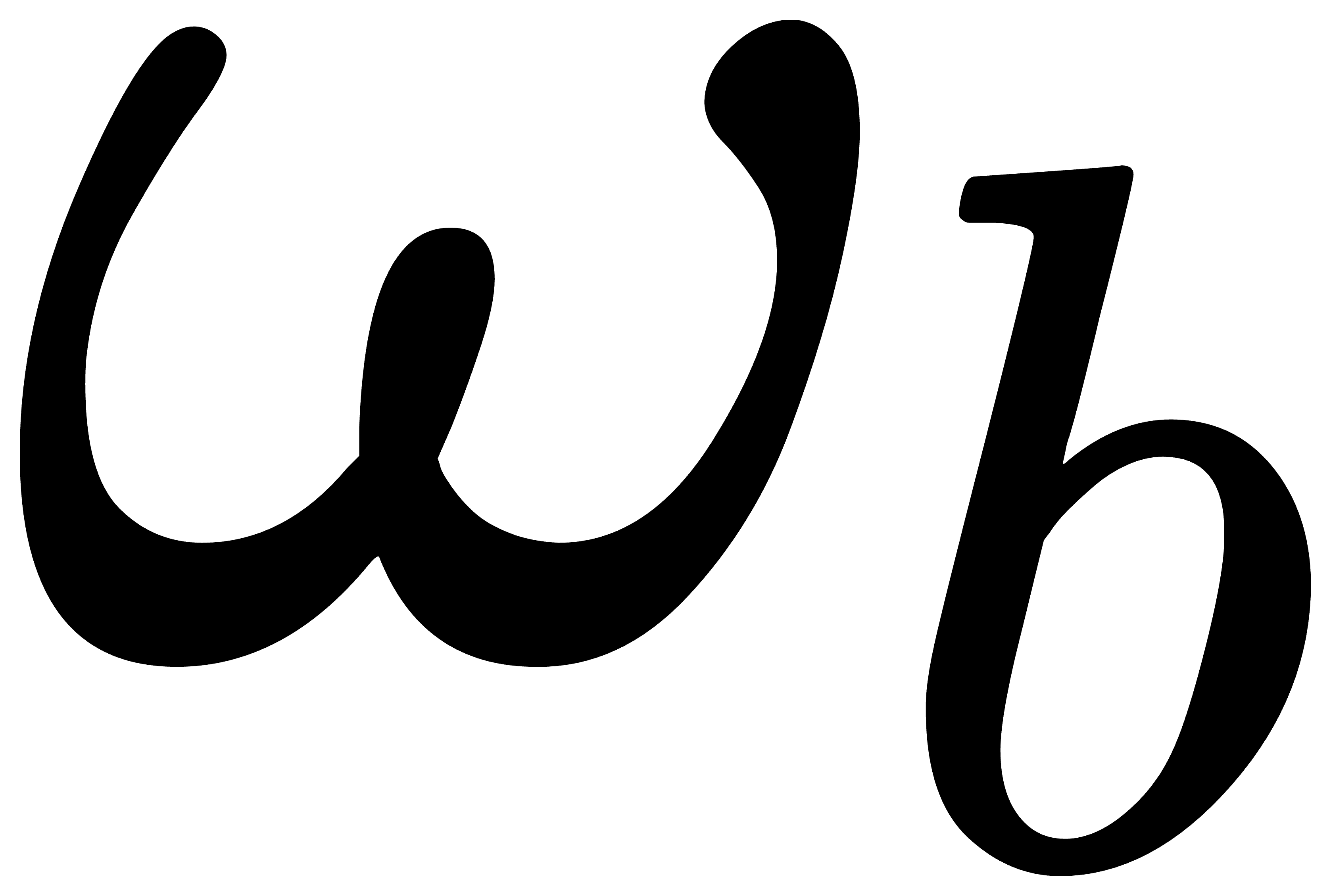：并不是相对动坐标系的角速度；确切地说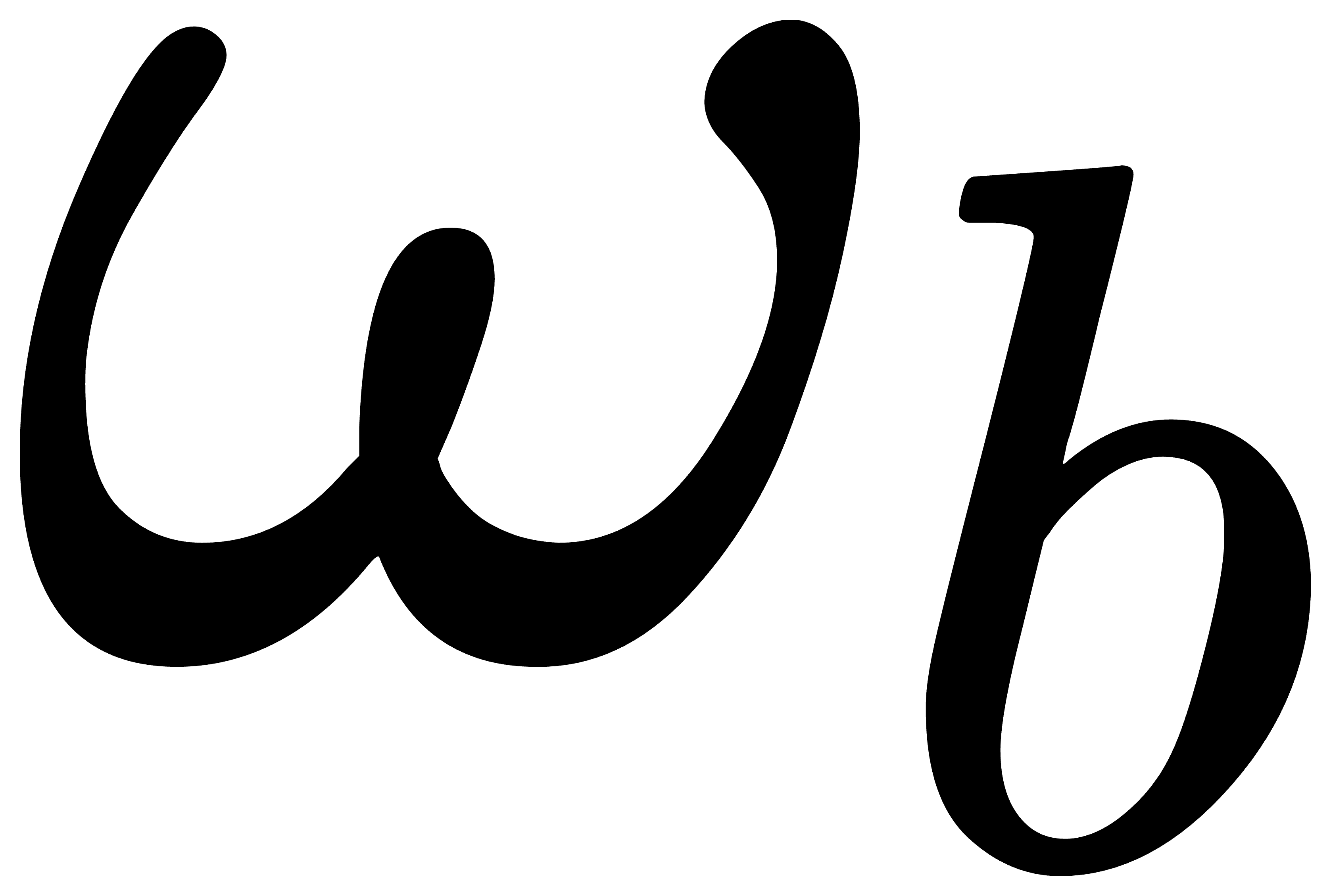， 表示的是相对静坐标系{b}的角速度，{b}只是与运动刚体随动坐标系瞬时重合。另外还需要注意一点，这里无论对 
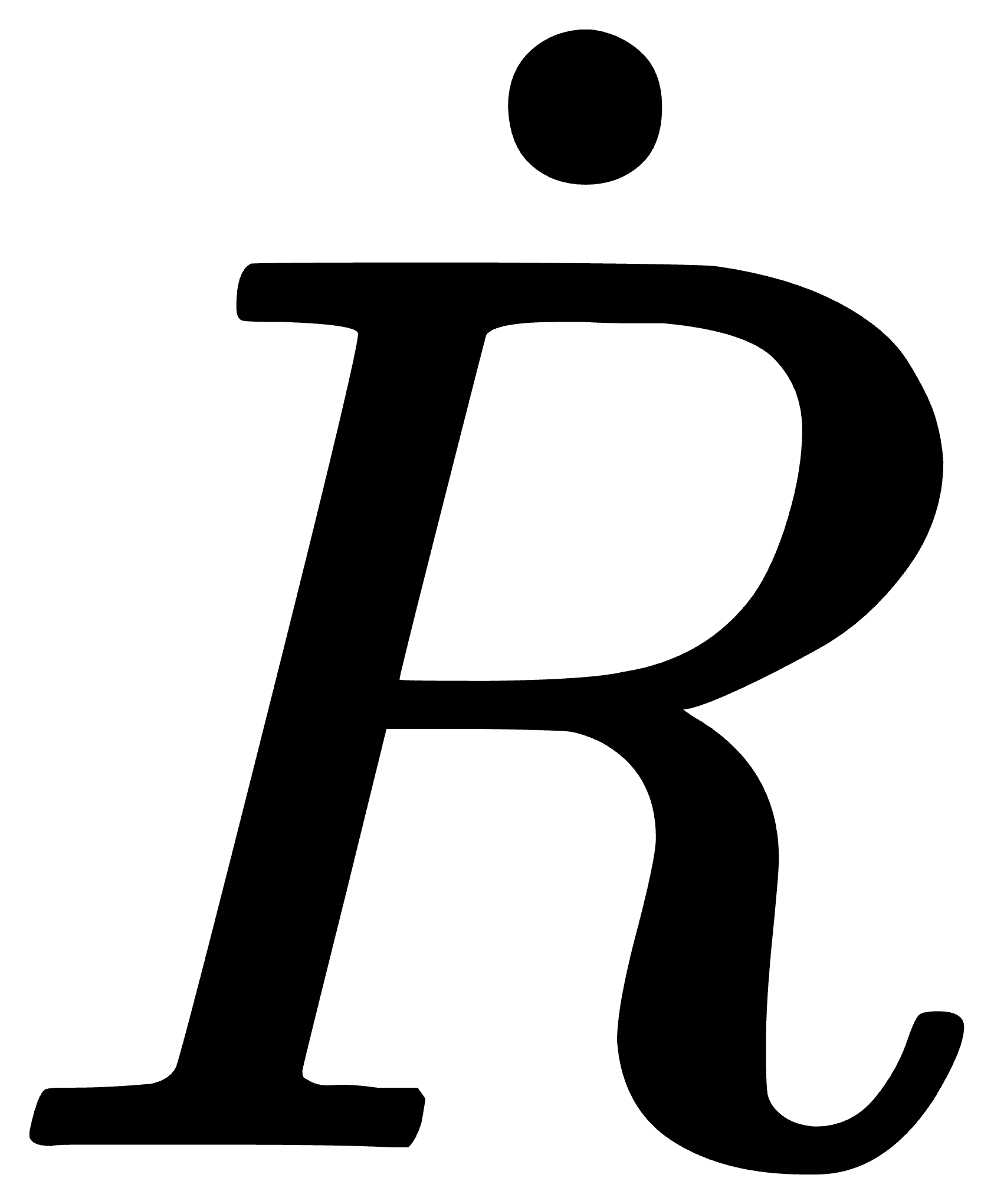左乘还是右乘 
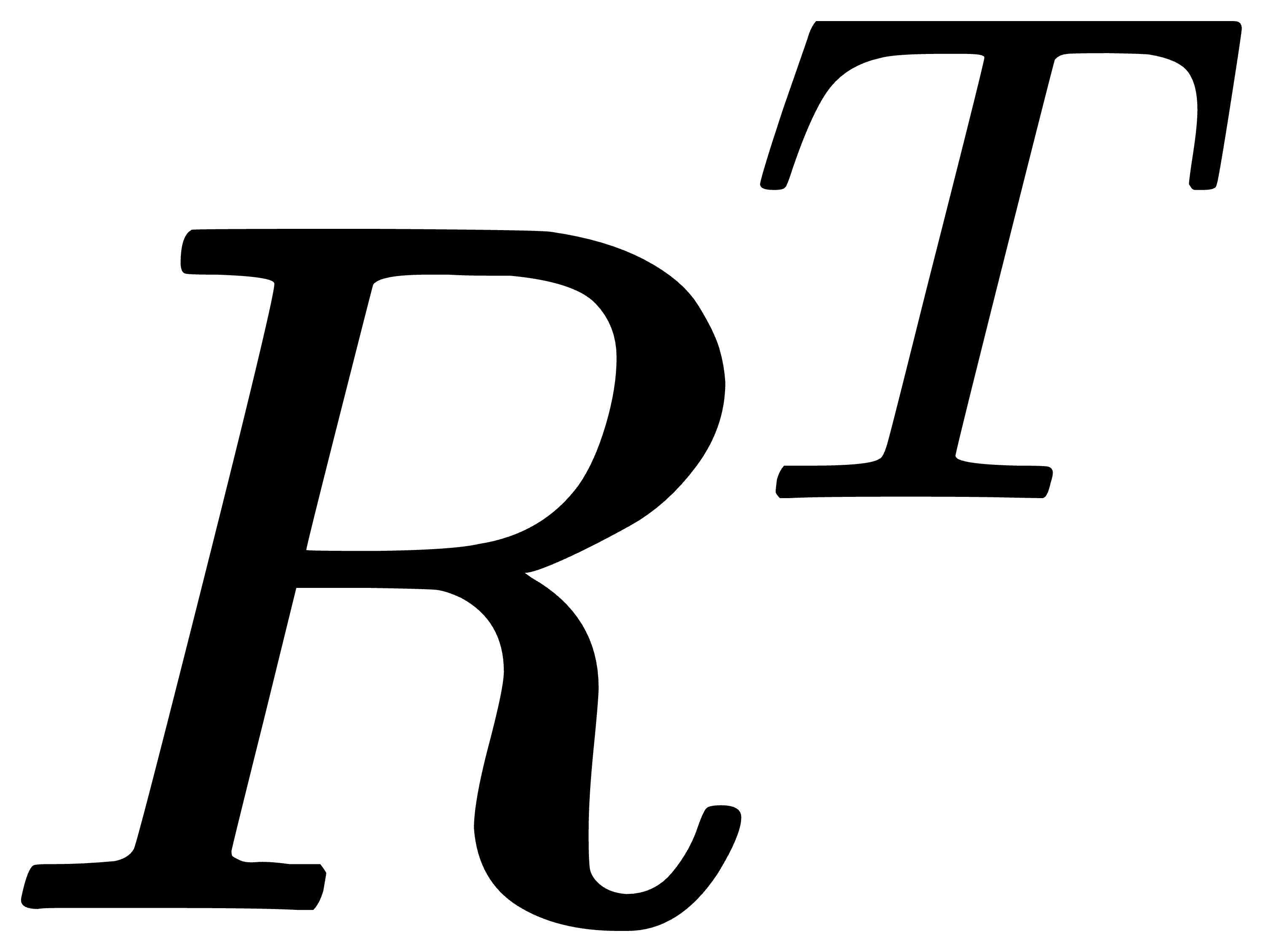都会得到有关角速度的一个反对称矩阵，只是相对的坐标系不同。
更容易理解的推导
根据坐标变换公式：
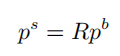
对上式左右同时求导:
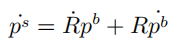
因为 p是附着在刚体上的, 所以p相对于刚体坐标系下的速度为0，故有
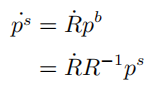
可以看出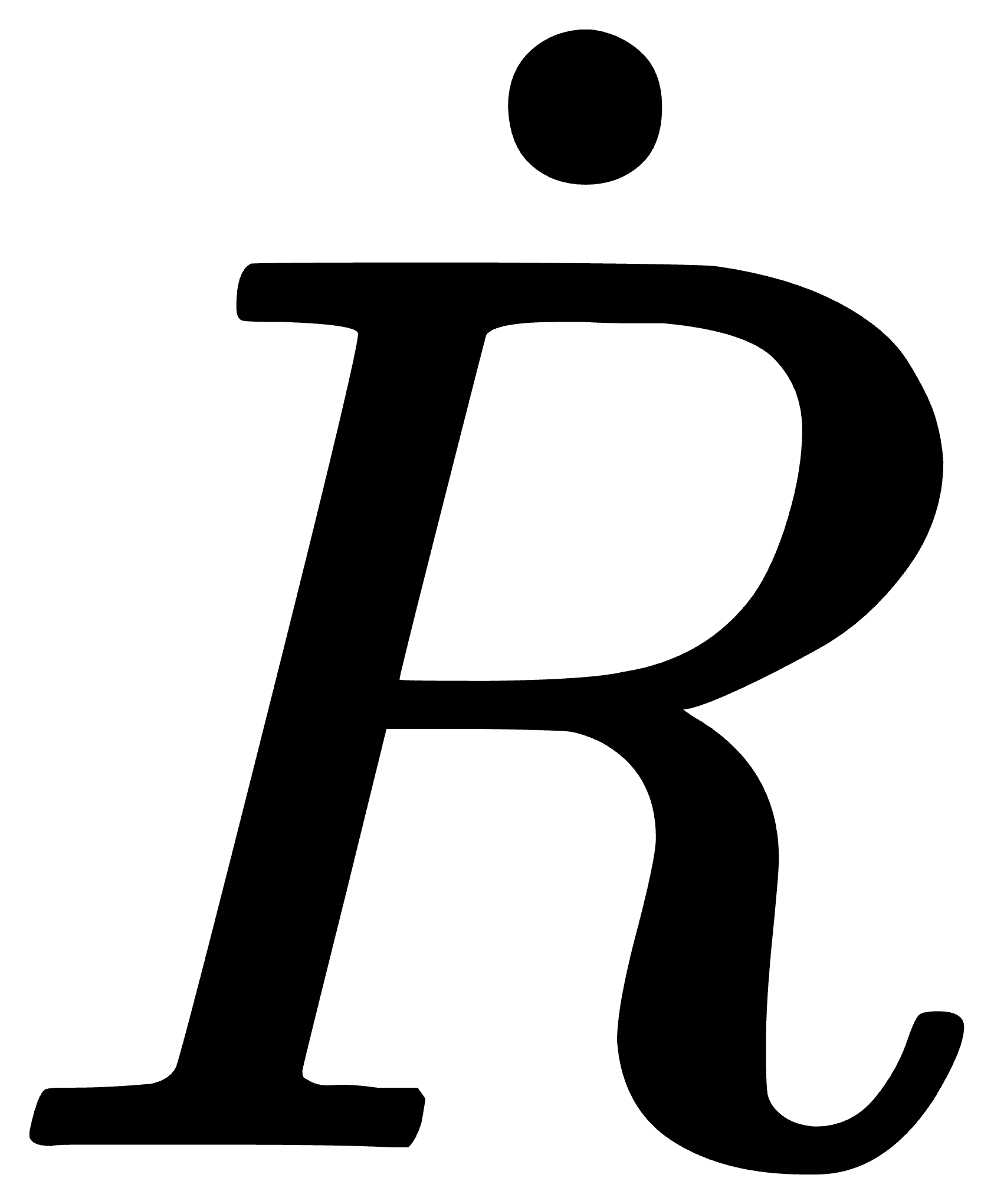 
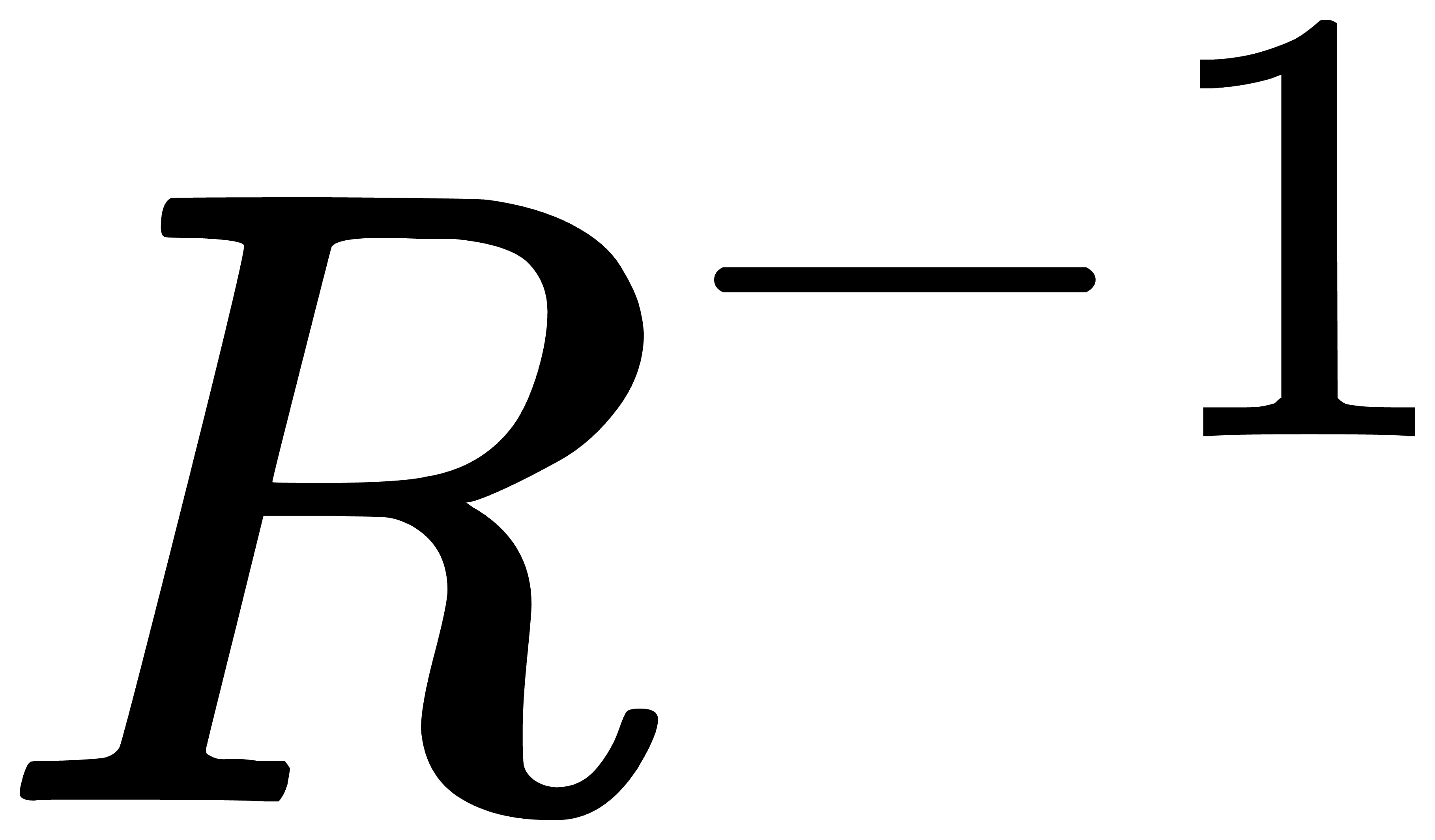将点的位置变成了点的线速度。又有角速度和线速度的公式:
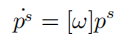
所以有空间角速度
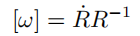
对于自己而言，这种方式推导出的结果，记忆效果最佳；
参考
[1] 现代机器人学
[2] 机器人学笔记——中科院软件所
