基于KDL与DH参数的运动学正逆解

简介
KDL 源码下载
SDH 参数作为运动学模型的输入
概念描述
正运动学求解器
逆运动学求解器
TRAC_IK逆解调用
- 参考代码示例
问题及解释
Gazebo 仿真部分
找不到要链接的动态链接库路径
- 注意事项
其他未归类事项
参考

简介

KDL（Kinematics and Dynamics）：机器人运动学与动力学组件，是MoveIt!中的默认运动学插件，在使用MoveIt Setup Assistant进行模型配置时，可以进行配置。学习机器人路径规划、轨迹规划、逆解算法，甚至编程的话，是一个很好的学习素材；本文的测试环境为： Ubuntu 20.04.2 ARM64, 以埃夫特机器人通用六轴工业机器人为例来说明如何调用KDL的正逆运动学求解部分; 下面简单对相关运动学求解器做个简单的介绍：

（1）KDL

KDL（Kinematics and Dynamics Library）是MoveIt!中的默认运动学插件，其有自己的优缺点，优点在于可求解封闭情况下逆运动，缺点在于速度慢，同时可能找不到解。

（2）TRAC-IK

TRAC-IK和KDL类似，也是一种基于数值解的运动学插件，但是在算法层面上进行了很多改进，求解效率高了很多。可通过如下方式安装（个人使用的是noetic版本）

sudo apt-get install ros-noetic-trac-ik-kinematics-plugin

（3）IKFAST

IKFAST是一种基于解析算法的运动学插件，可以求解任意复杂运动链的运动学方程并保证每次求解的一致性，整体来说，IKFAST比较稳定快速，一般5us的速度可完成运算。

3.MoveIt!运动插件开发方法

MoveIt!并不提供算法源码，只是将算法按照约定的方法进行封装，算法是数学模型的代码实现，和MoveIt!本身并没有关系，如果需要集成功能算法到MoveIt!中，需要编写接口文件，满足MoveIt!的插件规范即可，然后向move_group进行注册，这样使用时即可通过yaml或launch文件进行直接的调用。

KDL 源码下载

首先，下载KDL源码

cd ~/Destop
git clone https://github.com/SarvagyaVaish/Orocos-KDL-Forward-Kinematics.git

再需要安装相关依赖

sudo apt-get install liborocos-kdl-dev

第一步，确认是否配置成功，输入如下命令行

cd orocos_kinematics_dynamics/orocos_kdl/
mkdir build
cd build
cmake ..

后，会得到如下图像

然后在命令行中输入make,看编译是否成功，如下图所示

SDH 参数作为运动学模型的输入

在编写代码前，需要对DH参数进行转换，转换成KDL能够识别的内容，进行正逆运动学的计算，下面给出具体的代码(main.cpp)

#include <iostream>
#include <iomanip>

#include "chain.hpp"
// FK solver
#include  "chainfksolverpos_recursive.hpp"
// IK solver
#include "chainiksolverpos_lma.hpp"

using namespace KDL;
using namespace std;

const int JOINT_NUM = 6;
// ARC12-200 parameters
// input link and tool parameters;
 
const double L1  =  155.0;
const double L2  =  483.6;
const double L3  =    850;
const double L4  =  205.0;
const double L5  = 1000.0;
const double L6  =   75.0;
const double L7  =   -4.5;
const double PI2 =   PI/2;
// tool parameters
const double tool_x =  10;    
const double tool_y = -20;
const double tool_z =  30;
const double tool_a =  20;
const double tool_b =  10;
const double tool_c =  20;

double theta[JOINT_NUM]  = {0,  PI2, 0, PI, PI, PI};
double d[JOINT_NUM]      = {L2, L7, 0, L5, 0, L6};
double a[JOINT_NUM]      = {L1, L3, L4, 0, 0, 0};
double alpha[JOINT_NUM]  = {PI2, 0, PI2, PI2, PI2, 0};

Chain eftRobot() {
    Chain eft;
    eft.addSegment(Segment("joint1", Joint(Joint::RotZ),
                           Frame::DH(a[0], alpha[0], d[0], theta[0])));
    eft.addSegment(Segment("joint2", Joint(Joint::RotZ),
                           Frame::DH(a[1], alpha[1], d[1], theta[1])));
    eft.addSegment(Segment("joint3", Joint(Joint::RotZ),
                           Frame::DH(a[2], alpha[2], d[2], theta[2])));
    eft.addSegment(Segment("joint4", Joint(Joint::RotZ),
                           Frame::DH(a[3], alpha[3], d[3], theta[3])));
    eft.addSegment(Segment("joint5", Joint(Joint::RotZ),
                           Frame::DH(a[4], alpha[4], d[4], theta[4])));
    eft.addSegment(Segment("joint6", Joint(Joint::RotZ),
                           Frame::DH(a[5], alpha[5], d[5], theta[5])));
    return eft;
}

int main(int argc, char *argv[])
{
  double input_qj[JOINT_NUM];
	input_qj[0] =  0;
	input_qj[1] =  0;
	input_qj[2] =  0;
	input_qj[3] =  0;
	input_qj[4] = 50;
	input_qj[5] =  0;
	
	Chain eft_robot = eftRobot();
  JntArray q(eft_robot.getNrOfJoints());
	for(int i = 0; i < JOINT_NUM; i++)
	{
        q(i) = input_qj[i] * deg2rad;	
	}

 	ChainFkSolverPos_recursive fksolver(eft_robot);

    Frame flangeFrame;
	fksolver.JntToCart(q, flangeFrame);


    Frame toolFrame;
	toolFrame.p[0] = tool_x;
	toolFrame.p[1] = tool_y;
	toolFrame.p[2] = tool_z;
	Rotation toolRotation = Rotation::RPY(tool_a * deg2rad, tool_b * deg2rad, tool_c * deg2rad);
	toolFrame.M = toolRotation;

	Frame T;
	T = flangeFrame * toolFrame;
	Rotation R;
	R = T.M;
	double aa, bb, cc;
	R.GetRPY(cc, bb, aa);
	double A, B, C;
	A = aa * rad2deg;
	B = bb * rad2deg;
	C = cc * rad2deg;

	double fkRes[6];
	fkRes[0] = T.p[0];
	fkRes[1] = T.p[1];
	fkRes[2] = T.p[2];
	fkRes[3] = A;
	fkRes[4] = B;
	fkRes[5] = C;

    for (int i = 0; i < 6; i++) {
      cout << "fk value is " << fkRes[i] << endl;
    }
    
	// IK solve
	JntArray qInit(eft_robot.getNrOfJoints());
	for(int i = 0; i < JOINT_NUM; i++)
	{
        qInit(i) = input_qj[i] * deg2rad + 0.1;
	}
	JntArray qSol(eft_robot.getNrOfJoints());
	

	double eps = 1E-6;  // 笛卡尔空间的收敛阈值
	int maxIter = 500;
	double eps_joints= 1e-8;   // 关节空间的收敛阈值
	ChainIkSolverPos_LMA ikSolver = ChainIkSolverPos_LMA(eft_robot, eps, maxIter, eps_joints);
	ikSolver.CartToJnt(qInit, flangeFrame, qSol);
    std::cout <<"(KDL IK SOLVE)theta1 value is\t" <<  rad2deg * qSol(0)  << "\n";
    std::cout <<"(KDL IK SOLVE)theta2 value is\t" <<  rad2deg * qSol(1)  << "\n";
    std::cout <<"(KDL IK SOLVE)theta3 value is\t" <<  rad2deg * qSol(2)  << "\n";
    std::cout <<"(KDL IK SOLVE)theta4 value is\t" <<  rad2deg * qSol(3)  << "\n";
    std::cout <<"(KDL IK SOLVE)theta5 value is\t" <<  rad2deg * qSol(4)  << "\n";
    std::cout <<"(KDL IK SOLVE)theta6 value is\t" <<  rad2deg * qSol(5)  << "\n";

	return 0;
}

以及对应的CmakeLists.txt如下

cmake_minimum_required (VERSION 3.0.2)
project (FK_KDL_Tutorial)

find_package (orocos_kdl REQUIRED)
include_directories (${orocos_kdl_INCLUDE_DIRS})

add_executable (SimpleRobotFK main.cpp)
target_link_libraries (SimpleRobotFK ${orocos_kdl_LIBRARIES})

另外需要修改在最上层的CMakeLists.txt，加入build的目录，即可，如下所示

加入完这段指令后，回到build目录，输入cmake .., 在build目录中，能够看到如下内容(重要的就只有main.cpp与CMakeLists.txt了)

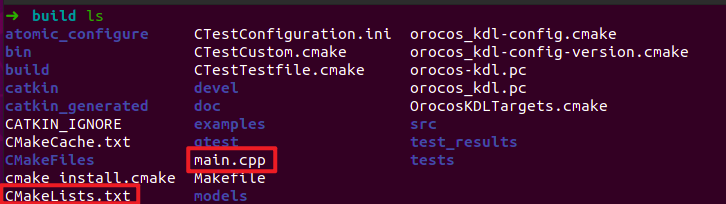
直接在命令行中make即可，如下图所示

这样就成功了，然后通过如下指令，运行编译出来的结果

cd ../devel/lib/orocos_kdl
./SimpleRobotFK

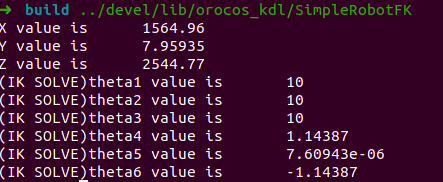
至此，基本上运动学正逆解部分就已经结束了，这里采用的是标准DH（SDH）建模，对于工业机器人来说，SDH和MDH其实差别不大，主要体现在机器人标定以及动力学递归推导的简洁性，当然，KDL里面也提供了MDH以及旋量等方式进行的运动学建模，仅作为示例，不一一列举；

概念描述

按照上面的例子，可以开始将这一工具用起来了，下面记录一些相关的概念；KDL描述机器人的方式分别是段，链，与树，可用于串并联机器人的描述；

机器人描述最小单元：Segment

机器人最小结构所需要的参数：关节、坐标、连杆质量、连杆惯性张量

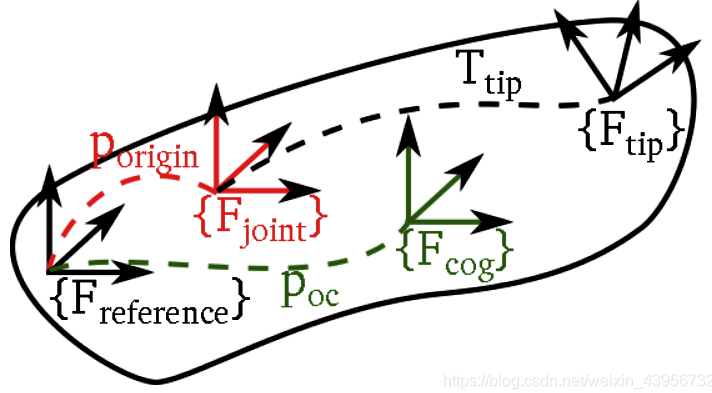
其中 oc表示质心；在图中可以看出，segment拥有一个参考坐标系、关节坐标系、质心坐标系，tip坐标系，其中参考坐标系通常与关节坐标系重合，tip坐标系用于描述杆件姿态，同时作为下一个segment的参考坐标系，质心坐标系与参考坐标系同向。在KDL中采用三个结构体来描述，关节、坐标，刚体惯量;

关节 joint描述

KDL源码对此部分的构造函数如下图所示

各个含义解释如下：

1 关节名字：name
2 原点：origin
3 轴：_axis
4 关节类型：JointType
JointType = Fixed （表示被固定的关节）

RotAxis
RotX
RotY
RotZ
TransAxis
TransX
TransY
TransZ
5 减速比：scale，一般默认设置就可以，需要注意的是KDL里面没有耦合比，要做电机关节转换的时候需要自己写一个函数；
6 偏置：offset
7 惯量：inertia，绕转动轴的一维惯量
8 阻尼：damping
9 刚度：stiffness

连杆动力学参数：RigidBodyInertia

连杆的动力学参数包括了三个量：

1 质量：m
2 质心：oc

3 惯性张量矩阵：Ic

RotationalInertia(double Ixx=0,double Iyy=0,double Izz=0,double Ixy=0,double Ixz=0,double Iyz=0)

串联机器人链：Chain

由基本元素段segment相连，构成了一个串联的链，

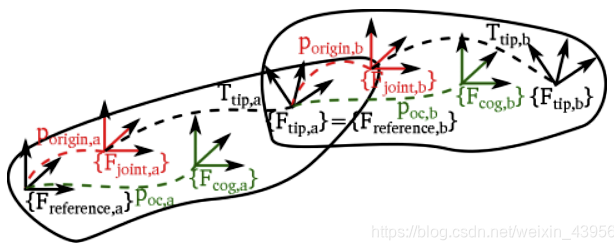
建立树：tree

一般，树不会直接代码建立，而是采用更简单的方法，通过URDF文件获取，获取方法如下所示。

from urdf_parser_py.urdf import URDF
from pykdl_utils.kdl_kinematics import KDLKinematics
from pykdl_utils.kdl_parser import kdl_tree_from_urdf_model

#读取URDF文件
robot = URDF.from_xml_file("/yourpath/catkin_ws/src/robot_description/armc_description/urdf/armc_description.urdf")

#将URDF转换为树
tree = kdl_tree_from_urdf_model(robot)

#截取需要的部分构成链
chain = tree.getChain("base_link", "sensor_link")

正运动学求解器

必须为每个链创建一个单独的求解器；
正运动学函数JntToCart(),从关节空间值计算笛卡尔空间值，逆运动学试用功能CartToJnt(),从笛卡尔空间值计算关节空间值；
KDL提供了关节运动学（从目前所看代码来说，并没有从电机角度到关节角度的转换，即无耦合比，但是有一个scale即传动比，所以推测是关节运动学）和动力学（关节动力学），考虑了从关节空间到笛卡尔空间的正逆运动学；
JntToCart方法：求解关节空间到某一个segment笛卡尔空间的正运动学（位置或速度）；当segmentNr=-1(默认值), 从基座解算到法兰端，当segmentNr>0如segmentNr=3时，对应的结果为$pc_{out} = T^0_3 = T^0_1T^1_2T^2_3$

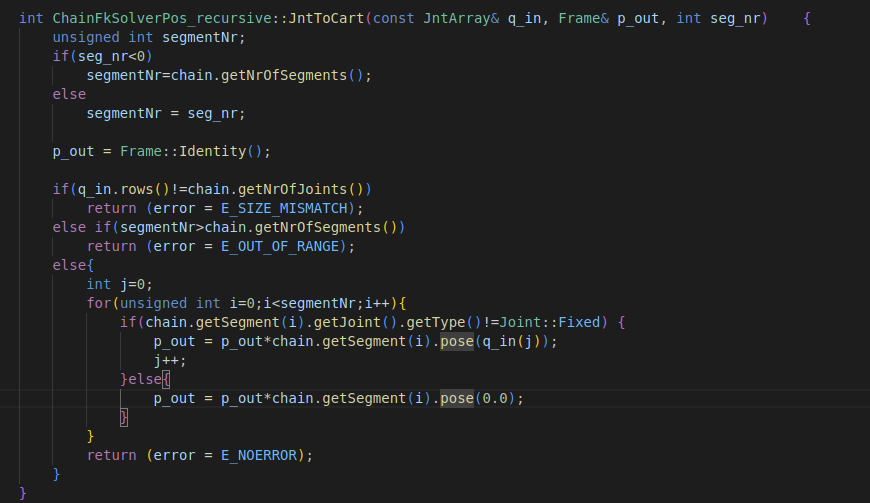
逆运动学求解器

chainIksolver.hpp中有两个抽象类

ChainIkSolverPos
ChainIkSolverVel
ChainIkSolverAcc(带有关节加速度约束的求解)

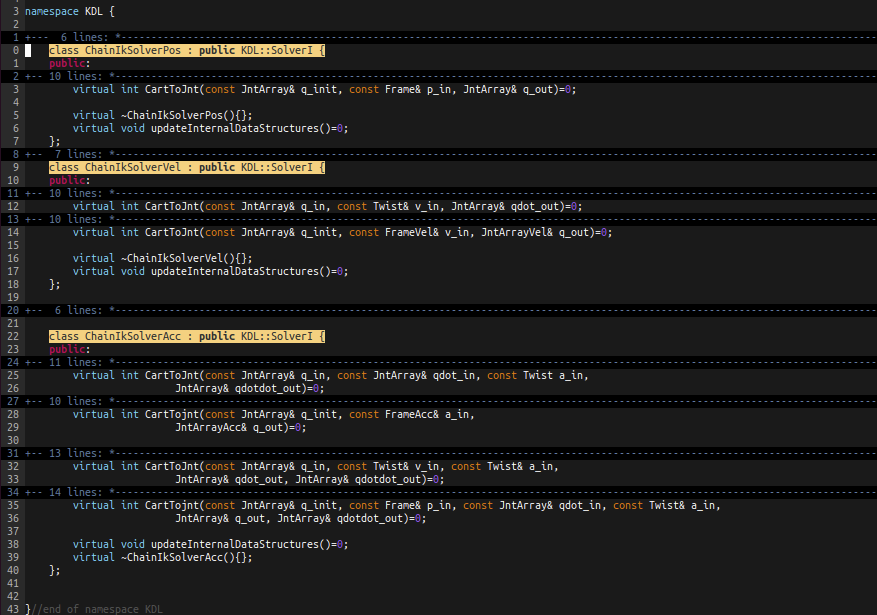
KDL逆解采用的数值解法其中：

位置求解有三种（Levenberg Marquardt(非线性最小二乘优化问题的算法, 结合了梯度下降和牛顿法的优点), Newton Raphson(基于泰勒展开的思想，将非线性函数线性化，从而在每次迭代中逐步逼近函数的根), Newton Raphson(关节限位))

速度求解有四种（SVD分解及其优化）

TRAC_IK逆解调用

参考代码示例

#include <ctime>
#include <iomanip>
#include <iostream>
#include <random>
#include <string>
#include <vector>
#include <random>
#include "chain.hpp"
#include "chainfksolverpos_recursive.hpp"
#include "optimal_ik.hpp"
#include <chrono>

using namespace EfortRobotics;
using namespace std;


std::vector<double> generateRandomNumbers(size_t N, double lower_bound,
                                          double upper_bound) {
  // Create a random device and use it to seed the random number generator
  std::random_device rd;
  std::mt19937 generator(rd());

  // Define the distribution range
  std::uniform_real_distribution<double> distribution(lower_bound, upper_bound);

  // Vector to store the random numbers
  std::vector<double> random_numbers;
  random_numbers.reserve(N);

  // Generate N random numbers
  for (size_t i = 0; i < N; ++i) {
    random_numbers.push_back(distribution(generator));
  }

  return random_numbers;
}

const double GR1650RobotData[10][15] = 
{{3.34794617,-10.58260822,8.23197365,-0.04651885,-1.02300739,-26.67648125,45.72592545,-41.07115173,-15.41529846,1455.87561,268.4154053,574.6983032,121.972,66.6175,93.079},
{3.34794617,-10.58260822,8.23197365,-0.21433127,-1.15195727,-26.62742043,45.64493942,-41.24930191,-15.33370686,1458.096802,264.3443298,572.6964722,121.972,66.6175,93.079},
{3.34794617,-10.58260822,8.23197365,-0.31202319,-1.22743583,-26.59846497,45.59809494,-41.35301208,-15.28658581,1459.392944,261.9689026,571.5285645,121.972,66.6175,93.079},
{3.34794617,-10.58260822,8.23197365,-0.47910076,-1.35722435,-26.54826355,45.51836777,-41.53038788,-15.20662689,1461.614624,257.8968201,569.5262451,121.972,66.6175,93.079},
{3.34794617,-10.58260822,8.23197365,-0.57634461,-1.43317449,-26.51864624,45.47224808,-41.63362122,-15.16045284,1462.910889,255.521225,568.3581543,121.972,66.6175,93.079},
{3.34794617,-10.58260822,8.23197365,-0.74264199,-1.56375742,-26.46731567,45.39375305,-41.81016541,-15.08209801,1465.132568,251.4491119,566.355835,121.972,66.6175,93.079},
{3.34794617,-10.58260822,8.23197365,-0.83942902,-1.64016712,-26.43704033,45.34833908,-41.91290665,-15.03684616,1466.428833,249.0735321,565.1878052,121.972,66.6175,93.079},
{3.34794617,-10.58260822,8.23197365,-1.00494194,-1.77153146,-26.38458061,45.27103424,-42.08860397,-14.96004868,1468.650513,245.0014191,563.1854858,121.972,66.6175,93.079},
{3.34794617,-10.58260822,8.23197365,-1.1012702,-1.84839332,-26.35364723,45.22629929,-42.19085312,-14.91569138,1469.946777,242.625824,562.0174561,121.972,66.6175,93.079},
{3.34794617,-10.58260822,8.23197365,-1.26599526,-1.98052692,-26.30005836,45.15014267,-42.36568832,-14.84040546,1472.168579,238.5537109,560.0151367,121.972,66.6175,93.079}};

int main(int argc, char* argv[]) {

  const int jointNum = 9;
  const int dataInputNumber = 10;


  const double theta[jointNum] = {0, 0, 0,  0,   90,  0,   -90,     0, -90};
  const double d[jointNum] =     {0, 0, 0,  0,    0,  0,  1500, 108.5,  87};
  const double a[jointNum] =     {0, 0, 0,  0, 1400,  0,     0,     0,   0};
  const double alpha[jointNum] = {0, 0, 0, 90,    0, 90,    70,   -70,   0};

  double tool_x=100, tool_y=101, tool_z=102;

  double low[jointNum] =   {3.34794617-1e-5,-10.58260822-1e-5,8.23197365-1e-5, -180*deg2rad, -180*deg2rad, -160*deg2rad, -180*deg2rad, -180*deg2rad, -360*deg2rad};
  double upper[jointNum] = {3.34794617,-10.58260822,8.23197365,  100*deg2rad,  180*deg2rad,  160*deg2rad,  180*deg2rad,  180*deg2rad,  360*deg2rad};
  double input_qt[dataInputNumber][jointNum];
  double qc[dataInputNumber][jointNum];

  // TRAC_IK 求解需要限定求解最大时间以及阈值（所求出的关节角度正解后与期望的法兰位置对比的偏差）
  double thr = 1e-5;
  double maxTime = 5e-5;
  
  Chain eft_robot;
  eft_robot.addRigidBody(RigidBody("base_link"));

    eft_robot.addRigidBody(RigidBody(Joint(Joint::TransX),
                                 Frame::DH(a[0], alpha[0], d[0], theta[0])));
    eft_robot.addRigidBody(RigidBody(Joint(Joint::TransY),
                                 Frame::DH(a[1], alpha[1], d[1], theta[1])));
    eft_robot.addRigidBody(RigidBody(Joint(Joint::TransZ),
                                 Frame::DH(a[2], alpha[2], d[2], theta[2])));
    for (int i = 3; i < jointNum; i++) {
      eft_robot.addRigidBody(RigidBody(Joint(Joint::RotZ),
                                   Frame::DH(a[i], alpha[i], d[i], theta[i])));
  }

  PosJ qLow(eft_robot.getJointNumbers());
  PosJ qUpper(eft_robot.getJointNumbers());

  for (int i = 0; i < eft_robot.getJointNumbers(); i++) {
    qLow(i) = low[i];
    qUpper(i) = upper[i];
  }

  double input_qj[500][jointNum];
  for (int i = 0; i < 500; i++) {
    for(int j = 0; j < 3; j++) {
		input_qj[i][j] = GR1650RobotData[i][j];
	}	
	for (int k = 3; k < jointNum; k++){
        input_qj[i][k] = GR1650RobotData[i][k] * deg2rad;
	}
	for (int m = 0; m < 6; m++){
		input_qt[i][m] = GR1650RobotData[i][m+jointNum];
	}
  }

  ChainFkSolverPos_recursive fksolver(eft_robot);
  PosJ q(eft_robot.getJointNumbers());

  Frame flangeFrame;
  // test it cost time;
  double aa, bb, cc;
  double A, B, C;
  double fkRes[6];
  auto fk_start = std::chrono::high_resolution_clock::now();
  const int LOOP_NUMBER = 200;
  const int COMPUTER_COUNT = dataInputNumber * LOOP_NUMBER;

  for (int k = 0; k < LOOP_NUMBER; k++) {
	  for (int i = 0; i < dataInputNumber; i++) {
		  for (int j = 0; j < jointNum; j++) {
			q(j) = input_qj[i][j];
		  }
		  fksolver.fk(q, flangeFrame);
	  }
  }

  auto fk_end = std::chrono::high_resolution_clock::now();
  auto fk_duration = std::chrono::duration_cast<std::chrono::microseconds>(fk_end - fk_start);

  double fk_sol_time = fk_duration.count() * 1.0 / COMPUTER_COUNT;
  std::cout << "正解函数执行耗时: " << fk_sol_time << " 微秒" << std::endl;

  PosJ qInit(eft_robot.getJointNumbers());
  auto ik_start = std::chrono::high_resolution_clock::now();
  OPTIMAL_IK::OPTIMAL_IK ik_solver_trac_ik(eft_robot, qLow, qUpper, maxTime, thr);
  
  PosJ result(eft_robot.getJointNumbers());
  int rc;
  int solFailNumber = 0;
  for (int k = 0; k < LOOP_NUMBER; k++) {
  std::vector<double> random_numbers = generateRandomNumbers(jointNum, -10, 10);
	  for (int i = 0; i < dataInputNumber; i++) {
		  for (int j = 0; j < jointNum; j++) {
			q(j) =input_qj[i][j];
		  }
          fksolver.fk(q, flangeFrame);
          for (int m = 0; m < jointNum; m++) {
	    	  qInit(m) = input_qj[i][m] + random_numbers[m] * deg2rad;
          }

		  rc = ik_solver_trac_ik.ik(qInit, flangeFrame, result);
		  if (rc < 0) {
			  solFailNumber += 1;
			//return -1;
		  }
	  }
  }

  auto ik_end = std::chrono::high_resolution_clock::now();
  auto ik_duration = std::chrono::duration_cast<std::chrono::microseconds>(ik_end - ik_start);
  double fk_ik_sol_time = ik_duration.count() * 1.0 / COMPUTER_COUNT;

  std::cout << "逆解失败次数 " << solFailNumber << std::endl;
  std::cout << "正解+逆解函数执行耗时: " << fk_ik_sol_time << " 微秒" << std::endl;

  return 0;
}

问题及解释

1.KDL的inverse Jacobian和TRAC_IK的inverse Jacobian区别？

TRAC_IK 主要使用了 KDL 的 ChainIkSolverVel_pinv 来计算雅可比矩阵的伪逆，并基于非线性优化库 NLOPT 来进行求解。具体来说，TRAC-IK 结合了 KDL 提供的伪逆方法和 NLOPT 的优化算法，来提高逆运动学求解的效率和成功率。所以并没有新的雅可比求解的方式。

2.KDL中的joint limit包括哪些？

KDL的关节限制仅用于求解的，比如求解带有关节限制情况下，可用KDL中的ChainIkSoverPos_NR_JL来计算；另外提供了锁轴的计算方式, 相关内容可直接去看源码。

3.KDL求解成功率低，你认为主要问题在哪儿？

个人认为主要问题在于初始猜测、奇异性、关节限制处理、数值稳定性(如迭代次数, 阈值的设定)和运动学链复杂性等因素。

4.TRAC-IK非线性求解中cost function是什么？约束条件包括哪些？

在 TRAC-IK 中，cost function 被定义为机器人位置和姿态（法兰端）与期望目标（如果带有工具参数，需要转到法兰端）之间的误差。

约束条件只有关节限制，通过成本函数与约束条件限制，然后调用开源的非线性优化求解器NLOPT来进行求解。

Gazebo 仿真部分

ERROR: cannot launch node of type [robot_state_publisher/state_publisher]:解决方法

解决方法为修改/launch/display.launch文件中的 robot_state_publisher节点的 type为“robot_state_publisher”即可。

demo_gazebo无法启动

所报的问题如下

Error [parser.cc:488] parse as old deprecated model file failed.
Error Code 4 Msg: Required attribute[filename] in element[plugin] is not specified in SDF.
Error Code 8 Msg: Error reading element <plugin>
Error Code 8 Msg: Error reading element <model>
Error Code 8 Msg: Error reading element <sdf>

解决方式，屏蔽掉相关代码，参考如下

<transmission name="trans_joint_6">
         <type>transmission_interface/SimpleTransmission</type>
        <joint name="joint_6">
              <hardwareInterface>hardware_interface/EffortJointInterface</hardwareInterface>
          </joint>
          <actuator name="joint_6_motor">
              <hardwareInterface>hardware_interface/EffortJointInterface</hardwareInterface>
              <mechanicalReduction>1</mechanicalReduction>
          </actuator>
      </transmission>
      <gazebo>
          <!--
          <plugin name="gazebo_ros_control">
              <robotNamespace>/</robotNamespace>
          </plugin>
          -->
      </gazebo>

但是屏蔽掉后，无法在gazebo中做控制, 最后还是要对此部分内容做修改，加入PID参数等。

gazebo仿真掉轴

排查是否由于使用solidworks导出文件有误

在gazebo中将重力(gravity)关闭，观察机器人是否正常起立, 若能正常起立，则为ros_gazebo_control部分没有配置好；ros_gazebo_control的控制参数形式如下：

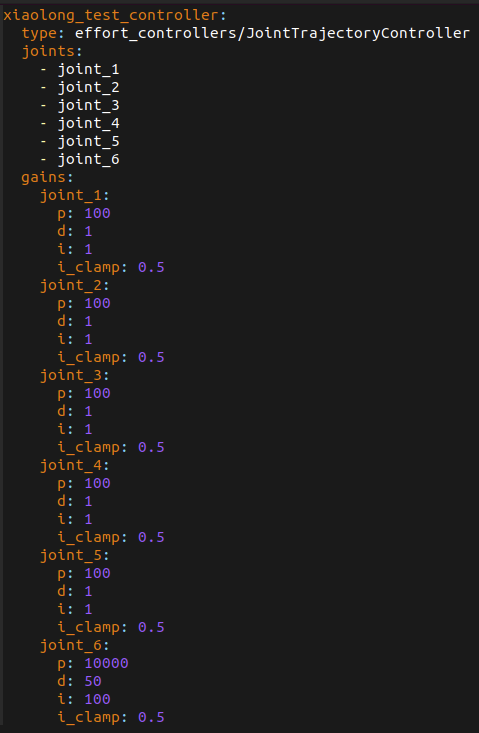
其中i_clamp为积分限幅（相当于死区控制），防止积分项过度累积，导致控制器输出不稳定的影响；

找不到要链接的动态链接库路径

编译正常，但是运行的时候会报出如下的错误

error while loading shared libraries: liborocos-kdl.so.1.5: cannot open shared object file: No such file or directory

那么在编译时需指明运行时链接的库的位置，参考代码如下所示(l为小写的L，且-Wl逗号后面不能有空格)

g++ main.cpp -lorocos-kdl -Wl,--rpath=/usr/local/lib

注意事项

在安装了ROS的情况下，KDL库的相关路径已经被添加到环境变量中，则可以直接链接，否则需要给出库的完整路径，此外，若有添加库路径到环境变量中的方法，应该也可以实现仅给出库的名称而不列出完整路径

其他未归类事项

建立软连接（用于自己修改KDL源码并在ROS中仿真）：

sudo ln -s /usr/local/lib/liborocos-kdl-models.so /usr/local/include/

参考

[1] Orocos-KDL-Forward-Kinematics

[2] 机器人KDL库（Kinematic Solvers）

[3] PyKDL—-运动段、运动链和运动树