转动的指数坐标表示
轴角解释
下面我们来介绍转动的三参数指数坐标表示。引人指数坐标，可以将旋转矩阵写成关于转轴（用单位向量
表示）和转角
的参数化形式，向量
就是该转动的三参数指数坐标表示形式。单独来写 和就是转动的轴-角(axis-angle)表示法。
旋转矩阵R的指数坐标表示 可以等效地解释如下。
• 单位转轴 和转角。坐标系最初与{s}重合，然后绕单位转轴旋转一定角度,最终相对{s}的姿态表示成R。
• {s}中表示的。坐标系最初与{s}重合，然后在单位时间内运动（即 在这一时间段的积分)，最终姿态表示成R。
• {s}中表示的。坐标系最初与{s}重合，然后在单位时间内运动（即 在这一时间段的积分)，最终姿态表示成R。
刚体转动的指数坐标
刚体转动的指数坐标可以等效成:
1, 单位转轴与绕该轴线的转角;
2, 通过连乘得到的三维向量。
Rodrigues’s formula
给定向量 
, 为任一标量， 而 为一单位向量，[]=[] so(3) 的矩阵指数为
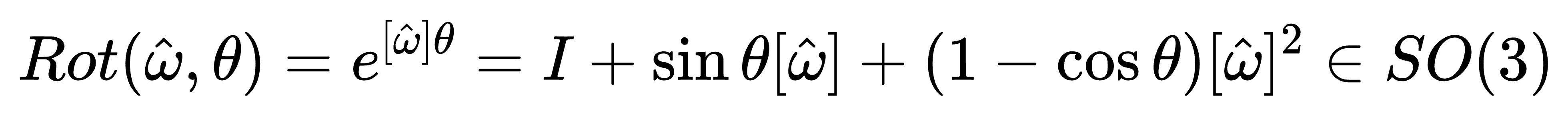
通常也被称为罗德里格斯公式(Rodrigues’s formula)。
以上给出了当给定转轴 和转角 时，如何通过矩阵指数构造旋转矩阵。进而, 物理量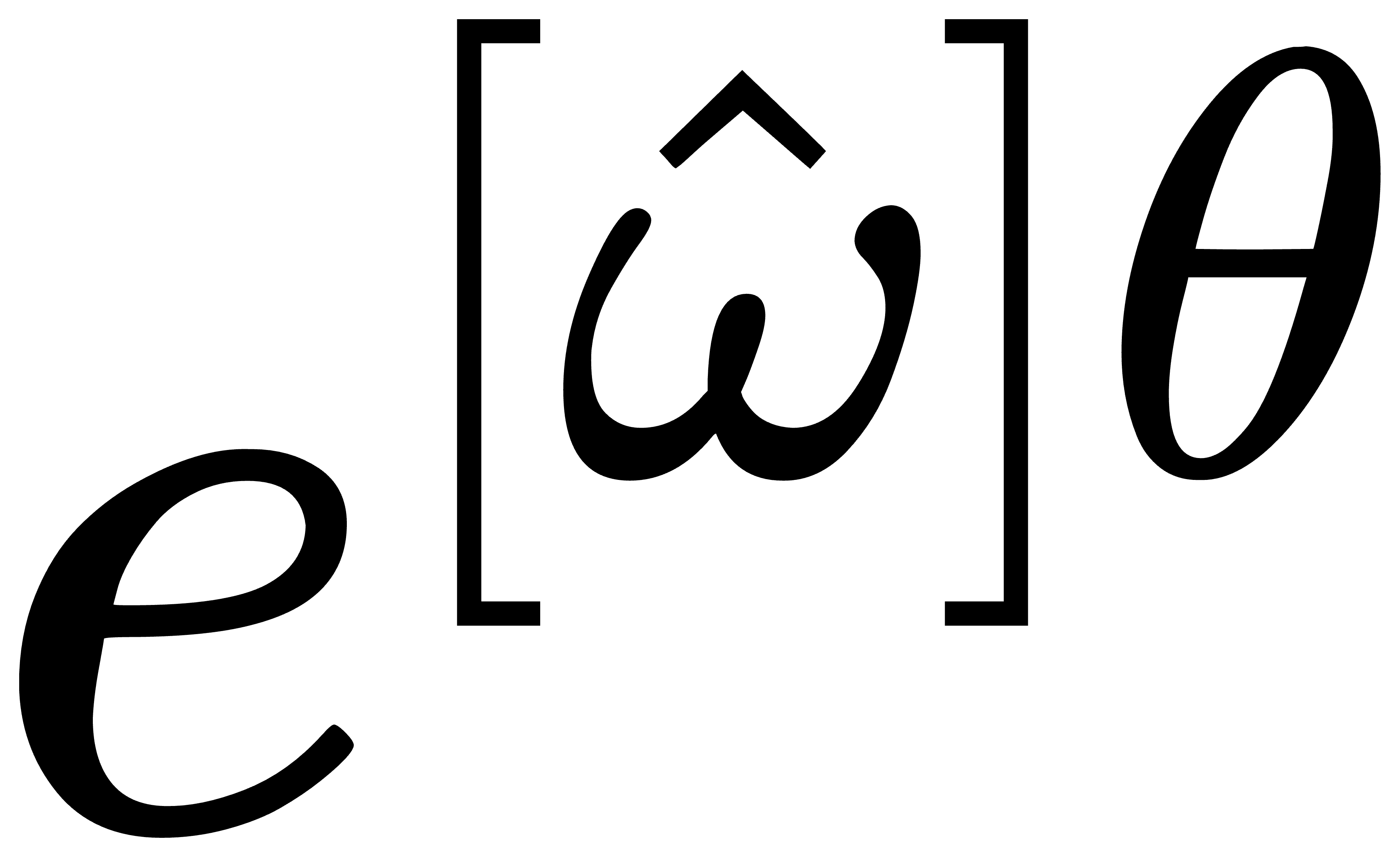 
p 可看成对向量p 绕转轴旋转角度后的结果。
参考
[1] May 2017 preprint of Modern Robotics, Lynch and Park, Cambridge U. Press, 2017. http://modernrobotics.org
