齐次变换矩阵
同时考虑刚体的位置和姿态。一种自然的选择就是用旋转矩阵R∈SO(3)表示物体坐标系{b}相对固定坐标系{s}的姿态,用向量p∈ 表示{b}的坐标原点相对{s}的坐标。所采用的方法不是将它们两者分离,而是集成在一个矩阵中。
表示{b}的坐标原点相对{s}的坐标。所采用的方法不是将它们两者分离,而是集成在一个矩阵中。
特殊欧氏群(special Euclidean group) SE(3)
特殊欧氏群(special Euclidean group)SE(3)亦称刚体运动(rigid-body motion)群或齐次变换矩阵(homogeneous transformation matrice)群,是所有4×4实矩阵T的集合,可以写成
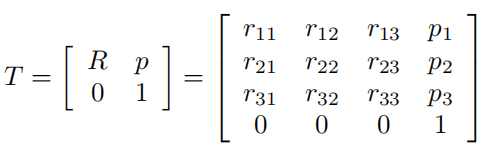
式中,R∈SO(3),p∈ 为列向量。
为列向量。
齐次变换矩阵的用途
如旋转矩阵一样,齐次变换矩阵T也有3种主要用途:
① 表示刚体的位形(位置和姿态);
② 变换参考坐标系(用向量或坐标系来表示):
③ 表示向量或坐标系的位移。
熟悉DH参数法建立运动学模型的对这块是非常熟悉了,所以就不介绍具体的示例了
运动旋量
运动旋量twist与旋量本身是两个东西,需要做一下区分,将运动旋量twist和时间系数的乘积定义为旋量,直观理解就是关于这个旋轴旋转了多少角度。旋量的矩阵形式通过指数运算就得到对应的位置变换矩阵;
用{s}和{b}分别代表固定(空间)坐标系和移动(物体)坐标系。不难得到有
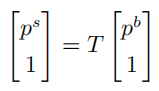
同时两边进行求导,有
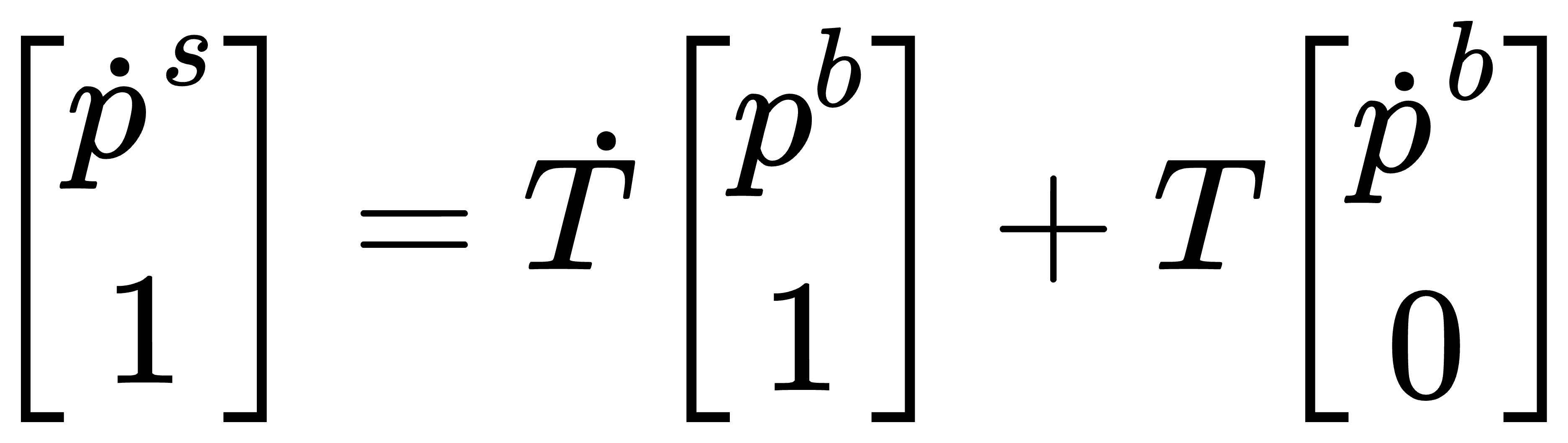
由于 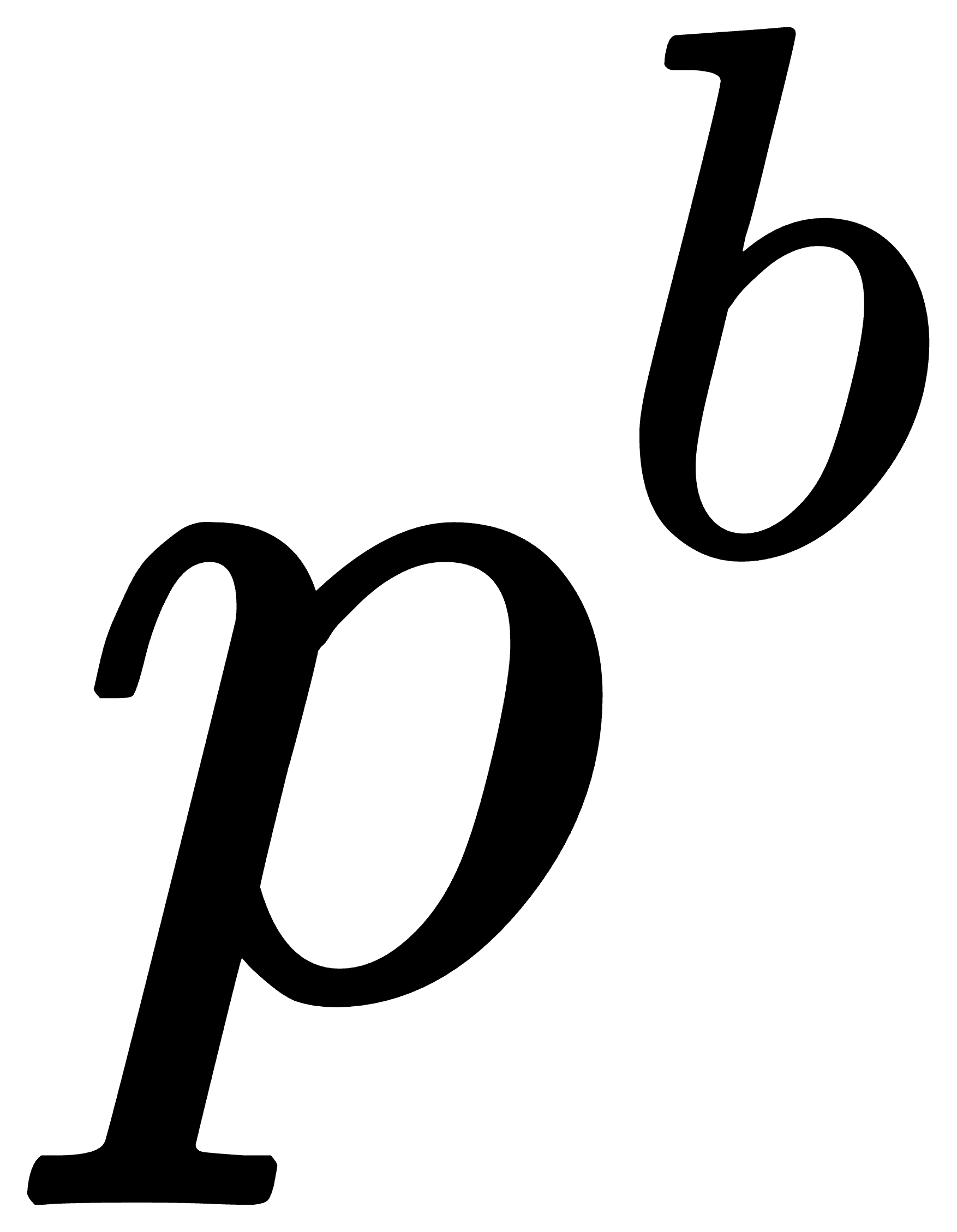 是固连{b}坐标系下的,所以其导数为0,不难得到有
是固连{b}坐标系下的,所以其导数为0,不难得到有
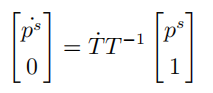
从上面式子可以知道, 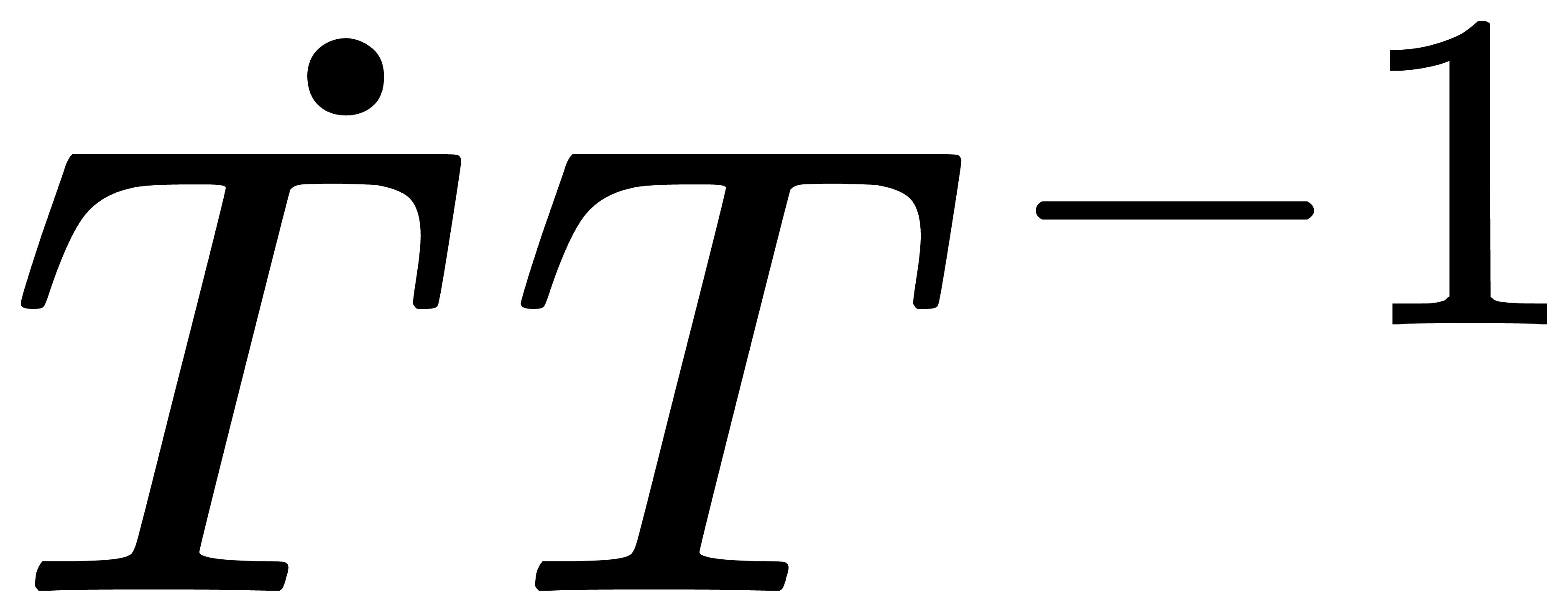 可以将空间点变成空间速度,由此定义运动旋量
可以将空间点变成空间速度,由此定义运动旋量
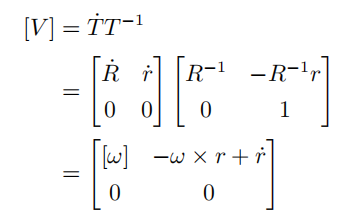
定义 twist V 为
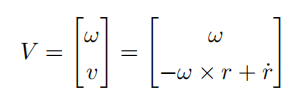
在 twist 中,v 是作为角速度的一个补充,通过矩阵乘法来得到线速度,它与角速度是互相独立的,它本身并不是刚体的线速度。v的几何解释是刚体上位于原点处的一个点的线速度。刚体本身是围绕 以单位角速度旋转的。
以单位角速度旋转的。
Twist 的坐标系变换
因为有:
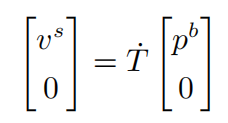
所以:
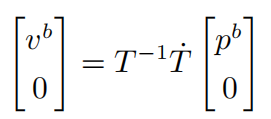
刚体坐标系下的 twist 矩阵为
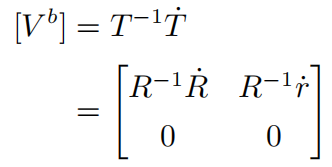
所以
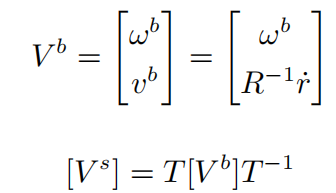
定义 T({b} 在 {s} 里的位姿表示)的伴随表示:
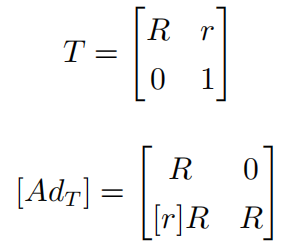
则
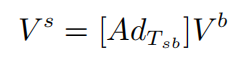
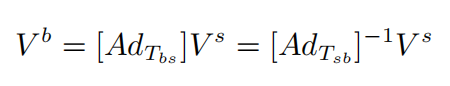
因为 screw axis 是单位 twist,所以变换公式也适用于 screw axis
参考
[1] <<机器人学笔记>> 许中兴, RISE 团队
