链表

线性表
- 链表
链表典型应用
参考

线性表

链表

与数组不同的是,组成链表的格子不是连续的。它们可以分布在内存的各个地方。这种不相邻的格子,就叫作结点。每个结点除了保存数据,它还保存着链表里的下一结点的内存地址。如下图所示：

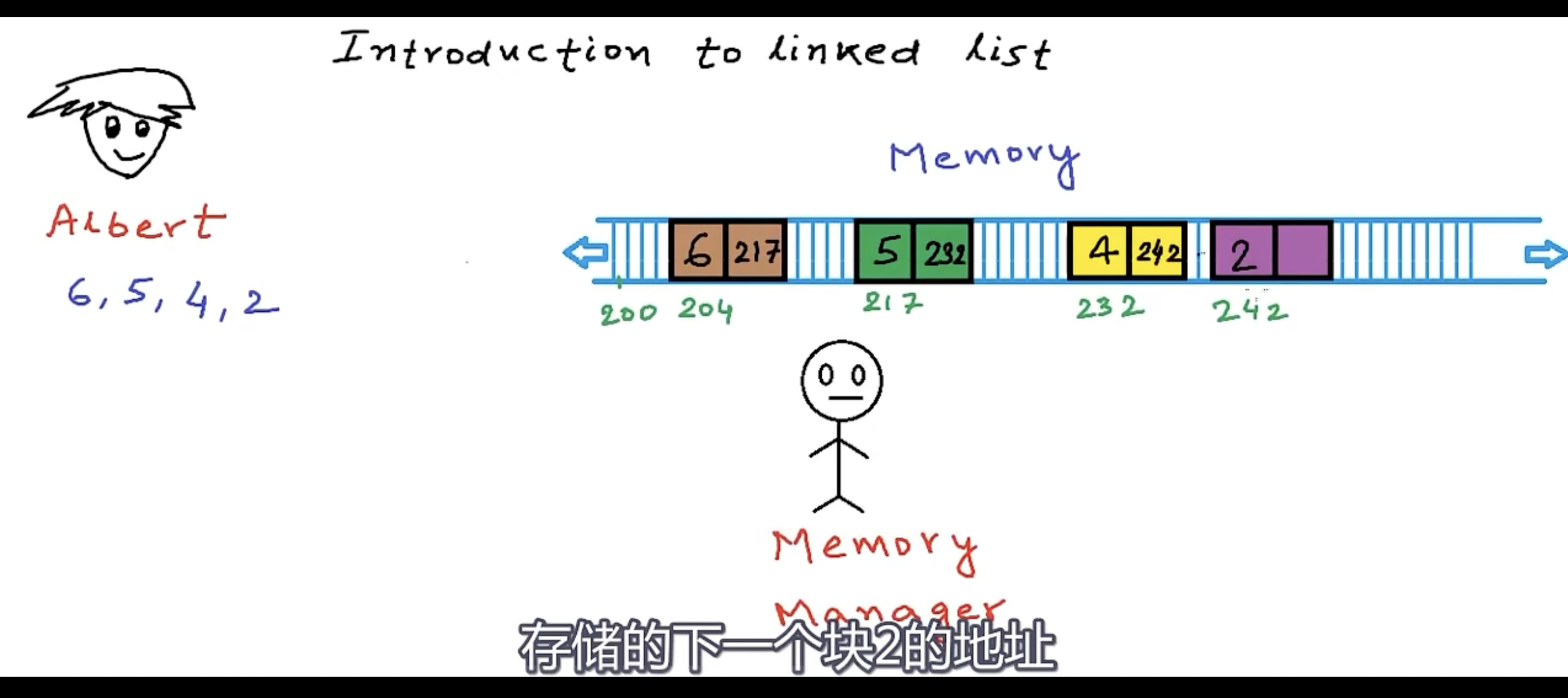
若想使用链表,只需知道第一个结点在内存的什么位置。因为每个结点都有指向下一结点的链,所以只要有给定的第一个结点,就可以用结点1的链找到结点2再用结点2的链找到结点3……如此遍历链表的剩余部分。下面这张图感觉更能形象的表述出这份意思

下面给出链表结构的C++代码实现部分

#include <iostream>

using namespace std;

// 节点类
class Node {
public:
    int data;
    Node* next;
    
    Node(int data) {
        this->data = data;
        this->next = NULL;
    }
};

// 链表类
class LinkedList {
public:
    Node* head;
    
    LinkedList() {
        this->head = NULL;
    }
    
    // 在链表末尾添加节点
    void append(int data) {
        Node* new_node = new Node(data);
        
        if (this->head == NULL) {
            this->head = new_node;
        } else {
            Node* current = this->head;
            while (current->next != NULL) {
                current = current->next;
            }
            current->next = new_node;
        }
    }
    
    // 在链表指定位置插入节点
    void insert(int data, int index) {
        Node* new_node = new Node(data);
        
        if (index == 0) {
            new_node->next = this->head;
            this->head = new_node;
        } else {
            Node* current = this->head;
            for (int i = 0; i < index-1; i++) {
                if (current == NULL) {
                    cout << "Error: Index out of range." << endl;
                    return;
                }
                current = current->next;
            }
            new_node->next = current->next;
            current->next = new_node;
        }
    }
    
    // 在链表指定位置删除节点
    void remove(int index) {
        if (this->head == NULL) {
            cout << "Error: List is empty." << endl;
            return;
        }
        
        if (index == 0) {
            Node* temp = this->head;
            this->head = this->head->next;
            delete temp;
        } else {
            Node* current = this->head;
            for (int i = 0; i < index-1; i++) {
                if (current == NULL) {
                    cout << "Error: Index out of range." << endl;
                    return;
                }
                current = current->next;
            }
            if (current->next == NULL) {
                cout << "Error: Index out of range." << endl;
                return;
            }
            Node* temp = current->next;
            current->next = temp->next;
            delete temp;
        }
    }
    
    // 显示链表中的所有节点
    void display() {
        Node* current = this->head;
        while (current != NULL) {
            cout << current->data << " ";
            current = current->next;
        }
        cout << endl;
    }
};

// 示例
int main() {
    LinkedList list;
    
    list.append(1);
    list.append(2);
    list.append(3);
    list.display(); // 输出：1 2 3
    
    list.insert(4, 1);
    list.display(); // 输出：1 4 2 3
    
    list.remove(2);
    list.display(); // 输出：1 4 3
    
    return 0;
}

链表典型应用

单向链表通常用于实现栈、队列、哈希表和图等数据结构。

栈与队列：当插入和删除操作都在链表的一端进行时，它表现出先进后出的特性，对应栈；当插入操作在链表的一端进行，删除操作在链表的另一端进行，它表现出先进先出的特性，对应队列。

哈希表：链式地址是解决哈希冲突的主流方案之一，在该方案中，所有冲突的元素都会被放到一个链表中。

图：邻接表是表示图的一种常用方式，其中图的每个顶点都与一个链表相关联，链表中的每个元素都代表与该顶点相连的其他顶点。

双向链表常用于需要快速查找前一个和后一个元素的场景。

高级数据结构：比如在红黑树、B 树中，我们需要访问节点的父节点，这可以通过在节点中保存一个指向父节点的引用来实现，类似于双向链表。

浏览器历史：在网页浏览器中，当用户点击前进或后退按钮时，浏览器需要知道用户访问过的前一个和后一个网页。双向链表的特性使得这种操作变得简单。

LRU 算法：在缓存淘汰（LRU）算法中，我们需要快速找到最近最少使用的数据，以及支持快速添加和删除节点。这时候使用双向链表就非常合适。

环形链表常用于需要周期性操作的场景，比如操作系统的资源调度。

时间片轮转调度算法：在操作系统中，时间片轮转调度算法是一种常见的 CPU 调度算法，它需要对一组进程进行循环。每个进程被赋予一个时间片，当时间片用完时，CPU 将切换到下一个进程。这种循环操作可以通过环形链表来实现。

数据缓冲区：在某些数据缓冲区的实现中，也可能会使用环形链表。比如在音频、视频播放器中，数据流可能会被分成多个缓冲块并放入一个环形链表，以便实现无缝播放。

参考

1, 《数据结构与算法图解》 — 杰伊温格罗著, 袁志鹏译
2, 《数据结构(C++语言版)》 — 邓俊辉编著
3, Hello 算法